Inscription / Connexion Nouveau Sujet
Problème QDM
Bonjour,
J'ai un 2eme problème sur un exercice sur le qdm en mécanique des fluides.
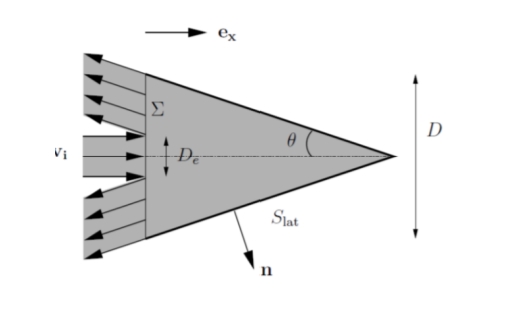
On considère un jet de diamètre De de fluide de masse volumique ρ incident avec une vitesse Ve
uniforme dans l'axe d'un cône de longueur L et d'ouverture θ. On suppose que le fluide ressort avec
une vitesse uniforme dans toute la surface complémentaire de la section d'entrée, parallèlement aux
parois du cône. On supposera le fluide parfait et incompressible. Le fluide rentre et sort à la pression
atmosphérique patm. On notera Σ la base du cône et Slat ses parois latérales. On cherche la force
exercée par le fluide + l'air ambiant sur le cône.
De= 10cm, D= 20cm, theta = 30°
On a donc P1, P2 et P3 = Patm et Ve = 1m/s
J'ai donc commencé par calculer la Vs avec la conservation du débit.
On a donc Ve* De² = Vs* ( D1+ D2 )²
D1 = diamètre du tube supérieur
D2 = diamètre du tube inférieur
D1= D2
Pour cela j'ai tout d'abord coupé le schéma en 2 et par symétrique c'est pareil en bas. J'ai donc
cos(thetha) = D1 / (D/2 - De/2 )
Cependant, ça m'a pas l'air vrai ...
Je vous remercie par avance
Pour la 2eme question, il faut faire un qdm avec
donc d'après l'exercice précédant :
avec
et
La Force est suivant ex car toutes les forces selon ey se compensent.
Jai donc comme vous pouvez le voir un problème avec Vs, je ne comprends pas trop.
Bonjour
Attention à ton calcul : D12+D22 (D1+D2)2
(D1+D2)2
D'autre part et surtout : la figure peut être trompeuse car elle représente une coupe du dispositif par un plan contenant l'axe de symétrie (Ox) du cône. La surface de sortie ne correspond pas à deux canalisations de diamètres respectifs D1 et D2 mais à une couronne de diamètre intérieur De et de diamètre extérieur D. Tu peux calculer l'aire Ss de cette couronne. Autre piège à éviter : la vitesse de sortie n'est pas perpendiculaire à la surface de sortie. Le débit volumique de sortie dépend du produit Ss.Vs mais aussi de l'angle  .
.
Ayant ainsi Vs, un raisonnement sur la variation de la quantité de mouvement du liquide permet d'obtenir le résultat recherché. Je ne vois pas l'intérêt de couper le cône en deux compte tenu de ce que j'ai écrit sur la surface de sortie.
Merci bcp
Il y a bien des pièges ...
Oui avec la formule
Qv =
Qv = Se*Ve = Ss*Vs*cos(thêta)
Avec Ss = pi (D²- De² )/4
Donc Vs = 0,38 m/s
Je ne suis pas sur si la normale pour Ss est bien perpendiculaire et non orienté pour Patm *Ss *n
Ainsi la force est présente sur x mais aussi sur y ?
Tu en en progression...
Je détecte juste un problème au niveau du terme :
L'écoulement du liquide sortant du cône admet l'axe (Ox) comme axe de symétrie pour les lignes de courant. Pour une goutte de liquide sortant en un point M de la surface de sortie  , correspond une autre goutte de fluide sortant un un point M' symétrique de M par rapport à l'axe Ox. Les vecteurs vitesses en M et en M' ont la même norme Vs mais ne sont pas colinéaires : leurs composante suivant -ex s'ajoutent mais leurs composantes radiales s'annulent. Dans la relation traduisant la variation de quantité de mouvement, il faut donc tenir compte uniquement de la composante de la vitesse de sortie selon ex...
, correspond une autre goutte de fluide sortant un un point M' symétrique de M par rapport à l'axe Ox. Les vecteurs vitesses en M et en M' ont la même norme Vs mais ne sont pas colinéaires : leurs composante suivant -ex s'ajoutent mais leurs composantes radiales s'annulent. Dans la relation traduisant la variation de quantité de mouvement, il faut donc tenir compte uniquement de la composante de la vitesse de sortie selon ex...
Merci
Oui d'accord j'ai compris donc aucune composante ey pour Vs car elles se compensent.
Ainsi Fcone -> eau = -25000 N
Négatif car la force est une reaction vers la gauche mais ça me paraît tout de même élevé (après le débit est quand même élevé 7,8 L/s)
J'obtiens une valeur de la force très inférieure à ton résultat. Tu peux poster ton résultat littéral après simplification.
Comme dans l'exercice précédent, la force est néanmoins relativement importante. Ne pas oublier qu'elle est en grande partie compensée par l'action de la pression atmosphérique sur la paroi extérieure du cône.
Ss = 0,0236 m²
Se = 7,85*10^-3 m²
Vs = 0,38 m/s
Ve = 1m/s
Patm = 1*10^5 Pa
Qv = 7,77 L/s
Dm = 1000* Qv = 7,77 kg/s
Donc
Je trouve maintenant F = -3,2*10^3 N
C'est donc moins grand.
Ne pas oublier qu'elle est en grande partie compensée par l'action de la pression atmosphérique sur la paroi extérieure du cône.
Donc comment on pourrait calculer cette Force dû à la pression extérieure ?
Ca m'amène donc à une autre question, la force qu'on a calculé, elle prend aussi en compte la force de l'air (pression atm) sur les paroi interne ?
D'accord maintenant avec toi !
Par application du principe des actions réciproques, tu obtiens :
Le cône est entièrement rempli d'eau en régime permanent étudié ici.
Il est donc soumis à trois forces :
- son poids auquel on ne s'intéresse pas ici ;
- l'action de l'eau sur le cône qui vient d'être étudiée ; il s'agit d'une force de pression exercée par l'eau sur la surface intérieure du cône ;
- l'action de l'air extérieur qui est une force pressante exercée sur la surface extérieure du cône.
Sans calcul, en raisonnant essentiellement sur les symétries du dispositif, je te laisse démontrer que cette force a pour expression :
Tu vas constater que cette force compense très largement l'action de l'eau sur le cône.
Son poids serait donc une force extérieure (rho g dv ) avec dv le volume dans ?
Oui, donc la force de l'air sur le cone est uniquement sur ex car les composantes sur ey sont nulles (elles se compensent).
J'ai un peu de mal à comprendre comment vous avez trouvé la surface ...
Mais sinon
F = 3,18*10^3 N donc oui ca compense bien.
aInsi la réélle force n'est que de 10N .
Il y a effectivement une astuce à connaître car utilisable à chaque fois que la pression est uniforme avec une surface pressée admettant un axe de symétrie (demie sphère, cône...).
Donc ici les composantes radiales des forces élémentaires se compensent deux à deux alors que les composantes suivant x s'ajoutent. La composante suivant x de dF est :
L'astuce apparaît maintenant : il faut remarquer que représente l'aire dS' du projeté orthogonal de la surface d'aire dS dans le plan contenant le disque
 formant la base du cône. La somme des dFx sur tout le cône représente donc simplement la force exercée par la pression atmosphérique sur la base
formant la base du cône. La somme des dFx sur tout le cône représente donc simplement la force exercée par la pression atmosphérique sur la base  du cône. D'où la formule que je t'ai fournie dans mon précédent message.
du cône. D'où la formule que je t'ai fournie dans mon précédent message.
D'accord , donc d'après ce que vous dites, la force de l'air suivant ex n'existe donc pas ? (Sur mon schéma, la flèche a gauche )
Tu ne m'a pas compris ! j'ai simplement démontré que cette force est orientée suivant et que son intensité (la norme du vecteur force) est égale à celle que la l'air exercerait sur un disque de diamètre D :
D'accord, je viens je pense de comprendre que la pression atm n'agit que sur une paroi solide (ici la surface latérale du cône pour simplifier ), elle ne peut pas agir sur une surface fictive (base du cône à l'air libre qui n'est donc pas solide ) C'est bien ça ?


