Voici mon énoncé:
Une boite de masse est placée sur une table. A l'intérieur de cette boite, une masse est fixée au couvercle par un ressort de raideur et de longueur au repos .
Quelle doit être l'amplitude minimale des oscillations verticales de la masse pour que la boite saute sur la table ? On suppose que les valeurs de , et de la hauteur de la boite sont suffisamment grande pour que la masse ne touche ni le couvercle, ni le sol.

----------------------
Voilà comment j'ai fait:
On prend comme repère avec pour origine le point d'attache entre le boite et le ressort et l'axe dirigé vers le bas.

Donc en j'étudie deux système, le système 1 qui est le mouvement de la masse qui est un oscillateur harmonique. Les forces appliqués sur sont le poid et la force de rappel
Donc l'équation du mouvement est et si la masse est en équillibre, on en tire que .

Pour les système 2, les forces agissant sur la boite sont le poids , la force exercé par le ressort sur la boite et la force exercé par la table sur la boite .

Dans mon corrigé, on me dit que mais que ces deux vecteur sont de directions opposés.

----------------------
Ma question
Pour moi, ces vecteur sont de même sens, et je ne comprend pas pourquoi il serait de sens opposé alors que si on fait un dessin, il sont bien dans le même sens.

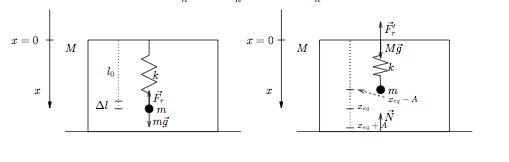
Voici en pièce jointe le schéma:
Merci