Inscription / Connexion Nouveau Sujet
problème équation différentielle
Bonjour je suis bloqué à un exercice de mécanique pouvez-vous m'aider ?
Voici l'énoncé:
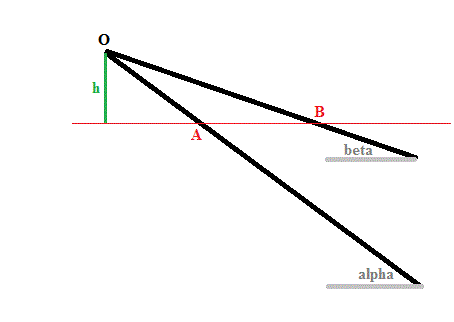
Deux billes sont lachéses simultanément, sans vitesse initialr, d'un point O sur deux glissières rectilignes de pentes différentes. On considère leur passage en deux point A et B situés sur la même horizontale. On néglige les frottements. Comparer en A et B:
1) Les accélérations des deux billes
2) Leurs temps de parcourt depuis O
3) Leurs vitesses
Où j'en suis:
1)
bille 1:
vec P1 + vec R1= m*vec a= m*d vec v/d vec t
Selon Ox: vec P1x=-mg cos (alpha)
vec R1x=0
m1*(d vec vx/dt)=-mg cos (alpha)
Selon Oy: vec P1y=-mg sin alpha
vec R1y=R1
m1*(d vec vy/dt)=R1-m1 g sin alpha
R1= m1 g sin alpha
On a d vec v1x/dt= g cos alpha= constante
on obtient v1x=(gcos alpha)t+C
avec v1x(t=0)=0=C
finalement v1x(t)=(g cos alpha)t
2) position:
d x1/dt=v1x(t)=g(cos alpha)t
x1(t)=(g cos alpha) t²/2+C
avec x1(t=0)=0=C
x1=(g cos alpha)t^2/2
en x1 (toa)=OA
OA= x1(toa)=(g cos alpha) (toa)²/2
 toa =
toa =  2 OA²/g cos alpha =
2 OA²/g cos alpha =  2 OA²/g OH
2 OA²/g OH
Pour les dimensions:
[ [ 2 OA/gOH]=([OA]/[g][OH])^1/2 = (T^-2)^1/2
2 OA/gOH]=([OA]/[g][OH])^1/2 = (T^-2)^1/2
3) vitesse:
v1x(toa)= 2g cos alpha OA =T =
2g cos alpha OA =T =  2 g OH
2 g OH
On a (d vec v1x/dt)/dt = g cos alpha = constante
Je ne connais pas grand chose en équation différentielle, j'espère avoir mis toutes les informations nécessaires.
je vous remercie d'avance
Si les billes glissent sans rouler :
accélération sur la piste OA : a1 = g.sin(alpha)
accélération sur la piste OB : a2 = g.sin(beta)
-----
OA = h/sin(alpha)
OA = a1 * t1²/2
h/sin(alpha) = g.sin(alpha) * t1²/2
t1² = 2h/(g.sin²(alpha))
temps de parcours OA
de manière analogue : temps de parcours OB
-----
v = a.t
v1 = a1*t1 = (vitesse de passage en A)
v2 = a2*t2 = (vitesse de passage en A)
-----
Si les billes roulent ... alors il faut tenir compte aussi de l'énergie de rotation.
... ce qui modifie toutes les réponses.
-----
Sauf distraction. 


