Inscription / Connexion Nouveau Sujet
Problème électrostatique
Bonjour,
Je dispose de l'énoncé suivant :
"On considère :
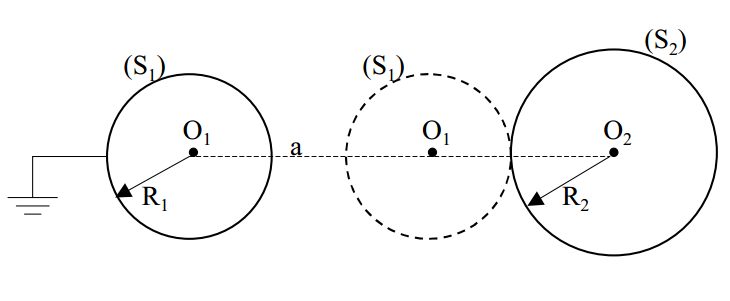
- une sphère (S1) conductrice de rayon R1 et de centre 01;
- une sphère (S2) conductrice de rayon R2 et de centre 02;
Etat électrostatique initial :
Les deux sphères sont placées dans le vide de telle sorte que la distance 0102 soit égale à a. (S1) est reliée à la terre et donc portée au potentiel 0. (S2) est isolée et porte la charge initiale Q2(0).
Exprimer la charge Q1(0) de (S1) en fonction de Q2(0), R1 et a. (J'ai réussi cette question, c'est après que je n'arrive pas).
1er contact avec (S2):
On amène (S1) au contact de (S2), avec (S1) qui n'est plus reliée à la terre. Une fois l'équilibre électrostatique atteint, déterminer, en fonction de Q2(0), a, R1 et R2, la nouvelle charge Q2(1) de (S2). La charge de (S2) a-t-elle augmenté ou diminué par rapport à l'état initial ?"
Je ne parviens à trouver Q2(1). La seule relation que j'ai à disposition est l'égalité :
Q1(0) + Q2(0) = Q1(1) + Q2(1) ... mais on nous demande après de déterminer Q1(1)...
Pouvez-vous m'aider SVP ? Merci 
Bonsoir,
Ta question n'a pas déclenché de réactions passionnées visiblement ...
Pour répondre à la question: à l'équilibre électrostatique:
- la charge est répartie en surface des conducteurs
- le champ électrostatique est nul à l'intérieur du conducteur
La surface de la réunion des 2 sphères est donc une équipotentielle:
On a donc V1(1) = V2(2)
Soit: Q1(1)/R1 = Q2(1)/R2
Est ce plus clair?
Merci beaucoup d'avoir répondu !
C'est plus clair maintenant oui  Mais comment lier Q1(1) à Q1(0) ? Puisque l'on doit exprimer Q2(1) en fonction de a, R1, R2 et Q2(0) ?
Mais comment lier Q1(1) à Q1(0) ? Puisque l'on doit exprimer Q2(1) en fonction de a, R1, R2 et Q2(0) ?
Bonjour
Tu as indiqué que tu avais pu lier à la première question Q1(0) à Q2(0)
(tu dois avoir qlq chose comme )
Tu sais, comme tu l'as justement écrit que:
Et depuis peu nous savons que
Tu as donc 3 équations qui doivent te permettre de tout exprimer en fonction de Q2(0)


