Inscription / Connexion Nouveau Sujet
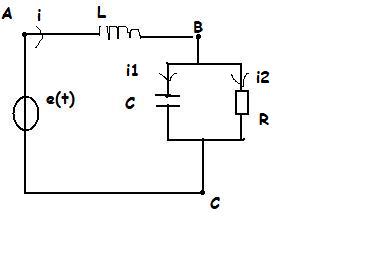
Problème dipole L série et RC parallèle
e(t) = E0sin(wt)
1°) Exprimer L en fonction de R, C et w(oméga) pour que le dipole soit équivalent à une résistance pure Req. Exprimer Req.
2°) Calculer L sachant que R=100 ohms, C=100/3 microF et w=400 rad/s.
3°) Détermienr la valeur efficace de I l'intensité du courant dans la bobine. Calculer sa valeur sachant que la valeur efficace de E vaut 180V.
4°) Exprimer les valeurs efficaces des différences de potentiel UAB et UBC. Application numérique.
5°)Déterminer les intensités complexes des courants i1 et i2 circulant respectivement dans la résistance et dans le condensateur. En déduire leurs valeurs efficaces et leurs déphasages par rapport à la tension en A et C. Apllication numérique.
6°) Calculer la puissance moyenne P sur une période consommée par le dipole AC.
d'habitude on dit bonjour voire bonne année !
pour la 1) il faut calculer la résistance équivalente entre A et C
la 2 est juste une application numérique
pour la suite il faut surement résoudre l'équa diff du circuit en i
Ouii désolé j'suis malpolie. En fait je bloque sur la résistance équivalente du fait qu'il y ait le bout du circuit en parallèle à droite. Je vois pas comment m'en sortir
c'est pas plus dur que ce que tu faisais en première sur les associations de résistance !
on t'a peut-être appris que quand on a deux résistance en parallèle on fait R1*R2/(R1+R2), ça se redémontre facilement
donc ici :
Req = jwL + (R/jCw)/(R + 1/jCw)
comprends, simplifie un peu tout ça et trouve la condition pour que ça soit purement résistif
bonsoir 
je reviens sur ce forum car j'ai le meme exercice et je bloque aussi sur la question 1)
j'ai compris que la resistance equivalente entre B et C etait r=(Rjcw+1)/(jcw) et que on additionnait Ljw et r car on les a en serie ! or je ne trouve pas la reponse souhaité , j'ai mis sous meme denominateur mais rien n'y fait ...
pouvez vous m'eclairer sil vous plait ?
Z = jwL + (R/(jwC))/(R + 1/(jwC))
Z = jwL + R/(1+jwRC)
Z = [jwL(1+jwRC)+R]/(1+jwRC)
Z = (jwL-w²RLC+R)/(1+jwRC)
Z = (jwL-w²RLC+R).(1-jwRC)/(1+w²R²C²)
Z = (jwL-w²RLC+R + w²RLC + jw³R²LC² - jwR²C)/(1+w²R²C²)
Z = (jwL +R + jw³R²LC² - jwR²C)/(1+w²R²C²)
Z = (R + j(wL + w³R²LC² - wR²C))/(1+w²R²C²)
Le dipole sera équivalent à une résistance pure si la partie imaginaire de Z est nulle, sonc si :
wL + w³R²LC² - wR²C = 0
Et comme w est différent de 0 ---> L + w²R²LC² - R²C = 0
L = R²C/(1+w²R²C²)
-----
Calculs à vérifier.
Bonjour
Est ce que la tension aux bornes de la bobine peut dépaser 180V.
J'ai trouvé R~ 36 ohm, I =5A, L=0.12henry
donc la tension aux bornes de la bobine 240V ?
Annuler
connectez vous