Niveau licence

Problème d'optique - défaut de l’œil

Posté par
huart 19-12-16 à 19:08

Bonjour à tous,

J'essaie d'aider une amie dans le cadre de son cours de physique en 1ère année médecine.
Malheureusement mes compétences en optiques ne sont plus aussi pointue que je l'aimerais.
Je sèche sur un des derniers problèmes présentés pour ce chapitre, en voici l'énoncé :

Tatie Gertrude a un pouvoir d'accommodation de 1δ. Elle peut, en plaçant les lunettes de sa nièce Josèphine (de puissance égale à -1.5 δ) à 2cm des yeux, voir nettement les dessins que son neveu Henry a faits sur le mur du fond du jardin (distance considérée infinie).
Quelles devraient être les corrections de ses verres (double foyer), placé à 1.5cm de ses yeux, pour qu'elle puisse voir les dessins d'Henry et finir la broderie de Joséphine (à 25cm de ses yeux)?

Je pensais commencer par calculer la puissance des lentilles, mais j'avoue que je m'y perds un peu. Si quelqu'un sait me donner un début de piste ca serait super !

Merci d'avance pour votre temps

Posté par re : Problème d'optique - défaut de l’œil 19-12-16 à 19:14

Citation :
Je pensais commencer par calculer la puissance des lentilles, mais j'avoue que je m'y perds un peu. Si quelqu'un sait me donner un début de piste ca serait super !

Je voulais dire le punctum remotum, et non pas la puissance qui elle est déjà connue

Posté par re : Problème d'optique - défaut de l’œil 20-12-16 à 22:16

Bonsoir
Pour les problèmes liés au port de lunettes, il y a une méthode simplifiée consistant à assimiler l'ensemble {cristallin - verre correcteur} comme un ensemble de deux lentilles accolées. La situation est alors assez simple car l'ensemble se comporte comme une seule lentille ayant pour vergence la somme des deux vergences. Ce n'est pas, me semble-t-il, la méthode demandée ici car la distance entre l'oeil et le verre correcteur est précisée et pas la même dans tous les cas... Le problème n'est pas alors tout à fait simple...
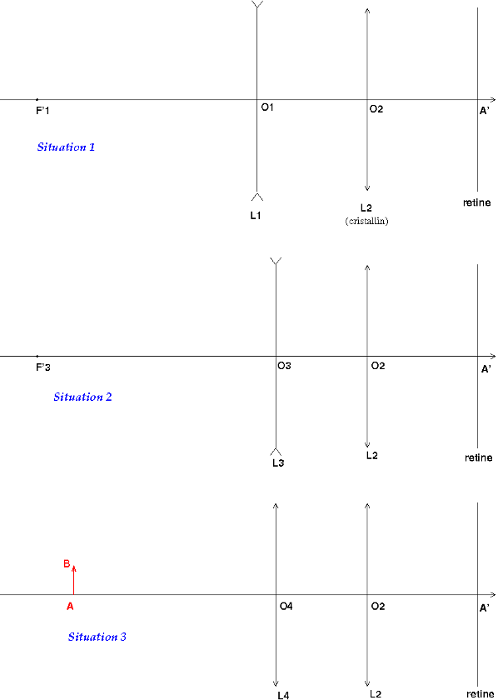
Situation n° 1 : L'œil cherche à voir le plus loin possible.La vergence du cristallin est la valeur la plus petite possible, notée V_min correspondant à son maximum de vision distincte. D'un point à l'infini sur l'axe optique, L1 donne une image confondue avec son foyer image F'1. F'1 est donc le "punctum remotum" de l'oeil.
Situation n° 2 : La lentille L1 est remplacée par la partie haute du verre correcteur progressif assimilé à une lentille divergente L3. L'image d'un objet à l'infini sur l'axe optique par L3 est le foyer image F'3 de L3 qui doit aussi être le "punctum remotum" de l'oeil. Conséquence :

$\overline{F_{1}^{,}O_{2}}=\overline{F_{3}^{,}O_{2}}\quad soit\quad\overline{F_{1}^{,}O_{1}}+\overline{O_{1}O_{2}}=\overline{F_{3}^{,}O_{3}}+\overline{O_{3}O_{2}}$

$\overline{F_{3}^{,}O_{3}}=\overline{F_{1}^{,}O_{1}}+\overline{O_{1}O_{2}}-\overline{O_{3}O_{2}}=\frac{1}{1,5}+2.10^{-2}-1,5.10^{-2}\approx0,672m$
D'où la vergence de la partie haute du verre correcteur :

$V_{3}=\frac{1}{\overline{O_{3}F_{3}^{,}}}=\frac{1}{-0,672}\approx-1,49\delta$
La relation de conjugaison de Descartes appliqué au cristallin L2 conduit à :

$\frac{1}{\overline{O_{2}A^{,}}}-\frac{1}{\overline{O_{2}F_{3}^{,}}}=V_{min}\quad donc\quad V_{min}-\frac{1}{\overline{O_{2}A^{,}}}=\frac{1}{\overline{F_{3}^{,}O_{2}}}=\frac{1}{\overline{F_{3}^{,}O_{3}}+\overline{O_{3}O_{2}}}=\frac{1}{0,672+1,5.10^{-2}}\approx1,46\delta$
Situation n° 3 : Un objet réel AB est placé à 25cm devant le cristallin donc 23,5cm devant le verre correcteur maintenant assimilé à une lentille convergence L4 de distance focale image f'₄. L4 donne de A une image A'₄ telle que :

$\frac{1}{\overline{O_{4}A_{4}^{,}}}-\frac{1}{\overline{O_{4}A}}=\frac{1}{f_{4}^{,}}\quad;\quad\overline{O_{4}A_{4}^{,}}=\frac{\overline{O_{4}A}\cdot f_{4}^{,}}{\overline{O_{4}A}+f_{4}^{,}}$
A'₄ est le "punctum proximum" de l'oeil. Le cristallin, dont la vergence est maintenant V_max=(V_min+pouvoir d'accommodation) donne de A'₄ une image en A'. La formule de conjugaison de Descartes donne :

$\frac{1}{\overline{O_{2}A^{,}}}-\frac{1}{\overline{O_{2}A_{4}^{,}}}=V_{max}\quad;\quad V_{max}-\frac{1}{\overline{O_{2}A^{,}}}=\frac{1}{\overline{A_{4}^{,}O_{2}}}\approx2,46\delta$
D'où la relation :

$\overline{A_{4}^{,}O_{2}}=\overline{A_{4}^{,}O_{4}}+\overline{O_{4}O_{2}}\quad;\quad\frac{1}{2,46}=-\frac{\overline{O_{4}A}\cdot f_{4}^{,}}{\overline{O_{4}A}+f_{4}^{,}}+1,5.10^{-2}\quad avec\quad\overline{O_{4}A}=-0,235m$
On en déduit la distance focale puis la vergence de la partie basse du verre progressif :

$f_{4}^{,}\approx0,586m\quad;\quad V_{4}\approx1,70\delta$
Pas évident pour un étudiant en première année de médecine dont la physique n'est pas la spécialité !
Je n'exclue pas quelques fautes de frappe ou erreurs de calculs mais la méthode me semble correcte... Les schémas ne sont pas à l'échelle bien sûr.

$Problème d\'optique - défaut de l’œil$