Inscription / Connexion Nouveau Sujet
Probleme d automatique
Bonjour,
Je permets de creer un topic d'automatique car en grande partie en faite c'est des maths.
A partir d'un circuit RLC on me demande de trouver:
-La representation externe du systeme (fonction de transfert).
-Déterminer une représentation d'etat sous forme campagne(forme canonique commande) du systeme
Merci
- Je pense avoir deja fais la premiere partie mais je suis pas sure je vais vous la mettre comme meme:
u(t)-ul(t)-ur(t)-uc(t)=0
u(t)-(L(di(t))/dt)-Ri(t)-y(t)=0
u(t)-(L(di(t)/(dt))-(RC(dy(t)/(dt))-y(t)=0
u(t)-(LC(d²y(t))/(dt²))-(RC(dy(t))/(dt))-y(t)=0
(LC(d²y(t))/(dt²))+(RC(dy(t))/(dt))+y(t)=u(t)
G(p)=Y(p)/U(p)
Fonction de transfert
LC Laplace(d²y(t))+RC laplace(((dy(t))/(dt))+Laplace(y(t))=Laplace(u(t))
Lcp²y(p)+Rcpy(p)+y(p)=u(p)
Y(p)/U(p)=1/(LcP²+RcP+1)
Voila ce que je trouve pour la fonction de transfert:
Y(p)/U(p)=1/(LcP²+RcP+1)
Merci de m'aider pour la suite
Parler de circuit RLC sans autre précision ne veut rien dire.
En voici quelques-uns (et il y a d'autres), ce sont tous des circuits RLC, inutile de dire que leurs fonctions de transfert sont différentes.

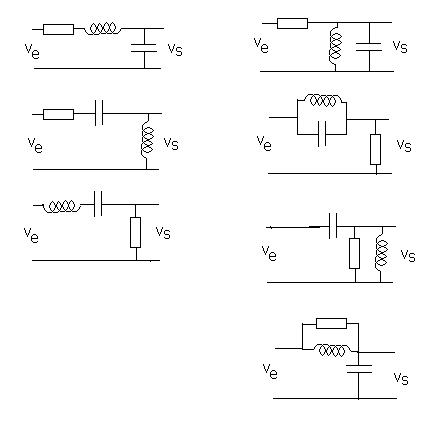
bonjour,
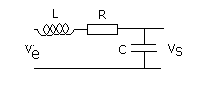
J'ai pas de chance mon circuit n'est pas representé.
Je vais vous l'expliquer car je sais pas comment vous avez fait pour dessiner.
La bobine (L) est en serie avec la résistance (R) et le condensateur (C) en paralléle.
J'espere que c clair
Re,
En faite c comme le premier mais il faut inverser la resistance et la bobine
S'il sagit du schéma ci-dessous:
vs/(1/pC) = ve/(R+pL + (1/pC))
vs/(1/pC) = ve/((pRC+p²LC + 1)/pC)
vs = ve/(pRC+p²LC + 1)
vs/ve = 1/(p²LC+pRC+1)
-----
Je ne connais pas le bidule "campagne" dont on parle plus loin.
J'ai beau être un habitué des automatismes, je ne connais cela.
-----
Sauf distraction. 
Ok merci c bien ce que j'ai trouvé pour le premier exercice.
Mais la c pas de l'automatisme mais que l'automatiQUE, j'ai eu la malheur de dire ca a ma prof en debut d'année.
Bonjour, pour donner la forme campagne, il faut commencer par mettre le système sous la forme d'une équation d'état.
Tu disposes dans ton circuit d'une inductance ainsi que d'un condensateur. Tu vas donc devoir considérer des variables d'état énergétique de type il et vc -respectivement le courant d'inductance et la tension aux bornes du condensateur- afin d'écrire l'équation d'état de la forme
Xpoint = A.X + B.U et Y=C.X+D.U
où
X est le vecteur d'état composé de il et de vc
Xpoint est la dérivée de X de composantes dil/dt et dvc/dt
U est le vecteur d'entrée (la tension Ve dans ce cas me semble-t-il)
C et D matrices (il se peut que D soit nulle)
Tu disposes d'une équation impliquant vc (et d'ailleurs, comme tu fais intervenir la dérivée seconde, ça ne m'étonnerait pas que vcpoint soit aussi une variable d'état), il te reste à écrire au moins une autre équation faisant intervenir il (exprimée en fonction des composantes de X et de U).
Matthieu.
Voila ce que je trouve pour la fonction de transfert:
Y(p)/U(p)=1/(LcP²+RcP+1)
-Déterminer une représentation d'etat sous forme campagne(forme canonique commande) du systeme:
Lcp²y(p)+RCpy(p)+y(p)=U(p)
(Lc (d²y(t))/(dt²))+Rc (dy(t))/(dt)+y(t)=u(t)
x1=y(t)
x2=(dy(t))/(dt)
x3=(d²y(t))/(dt²)
x1point=x2
x2point=x3
x3point=-LCx1-Rcx2-x3+U(t)
Representation d'etat:
x1point=x2
x2point=x3
x3point=-Lcx1-Rcx2-x3+U(t)
y(t)=x
Pouvez vous me dire si cela et bon. Il me reste le calcul de matrice que je ne sais pas effectuer. Merci de votre aide
Bonjour,
Il y a une erreur dans ton écriture de x3point car tu tentes d'exprimer la dérivée seconde de y càd x3 (et non x3point) en fonction des autres composantes.
Voici ce que je te propose :
donc
D'autre part, on a donc
donc en notant et
le vecteur d'état et sa dérivée,
puis en considérant que la sortie , tu dois être en mesure d'écrire les matrices A (3x3), B (3*1) et C (1*3) (D étant nulle)
Reste à voir quelle est la forme d'une matrice campagne ...
Dis-moi ce que tu en penses,
Matthieu


