Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Problème calcul de moment intérieur

Posté par
Newday 31-10-20 à 13:13

Bonjour,

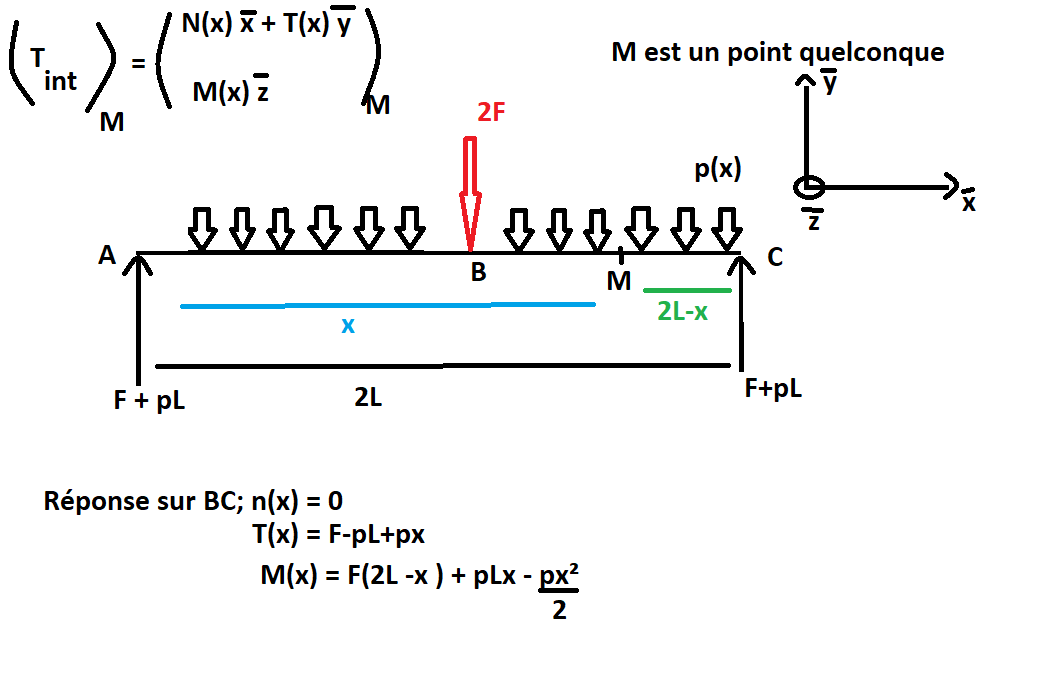
Pour cet exercice, on doit calculer les différentes résultantes et moment d'un torseur mécanique intérieur sur BC, sachant que p est une force uniformément réparti  , (voir la pièce jointe)

Voici mes calculs;
Pour N(x) = 0 c'est triviale, il n'y a pas de forces sur l'axe des x.
Pour T(x): on a T(x) = F+ pL + \int_{}^{2L-x}{-pdx} = F+pL -p2L+px = F-pL +px
ce qui est bien la réponse attendu.

Pour M(x), cependant j'ai un problème: j'ai fait
M(x) = MC\wedge T(x) = (2L-x)\wedge((F+pL)+\int_{}^{2L-x}{-pdx})

=(2L-x)(F+pL) + (2L-x)*\int_{}^{2L-x}{-pdx})

= F(2L-x) +pL(2L-x)+\int_{}^{2L-x}{-p(2L-x)dx})

=  F(2L-x) +pL(2L-x)+\int_{}^{2L-x}{-p(2L)dx}) +\int_{}^{2L-x}{pxdx})

=  F(2L-x) +pL(2L-x)-2pL(2L-x)+ p\frac{(2L-x)²}{2}

et là ça c'est faux car en développant j'obtiens +px²/2 au lieu de  -px²/2

Pourriez vous m'aider ?

Merci d'avance pour vos réponses

Problème calcul de moment intérieur

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 31-10-20 à 13:17

Bonjour,

Pour ne pas me planter, quels sont les appuis en A et B ?

Posté par
Newdayre : Problème calcul de moment intérieur 31-10-20 à 14:07

Bonjour,

C'est un appui simple, d'ou la seule composante sur y en A et  B  

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 31-10-20 à 14:43

OK, merci pour la précision.

Pour ma part, je procède par une méthode semi-analytique (en regardant ce qui se passe à droite de la coupure fictive) :

x [BC]

Ty(x) = F + p.L - p.(2L-x)

Mfz(x) = +(F+p.L) \times (2L-x) - p.\dfrac{(2L-x)^2}{2}

x [AB]

Ty(x) = F + p.L - p.(2L-x) - 2F

Mfz(x) = +(F+p.L) \times (2L-x) - p.\dfrac{(2L-x)^2}{2} - 2F \times (2L -x)


Vérification : \dfrac{dMfz}{dx} = -Ty

Posté par
Newdayre : Problème calcul de moment intérieur 31-10-20 à 15:05

Merci pour votre réponse,

Mais on doit absolument utiliser la méthode d'intégration pour retrouver ce M(x) à la fin, et j'arrive pas à trouver ou je me suis planter

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 31-10-20 à 15:18

C'est pénible ces manies d'obliger les étudiants à dérouler des méthodes calculatoires quand un simple schéma suffit ... Bref, passons

J'ai quelques commentaires sur ton calcul :
- il manque une borne d'intégration ;
- as-tu vérifié si l'erreur ne viendrait pas du produit vectoriel (suivant le sens parcouru dans le repère) ?
- tu cherches à regarder à droite ou à gauche de la coupure (car en fonction, le torseur de cohésion change de signe)

Posté par
Newdayre : Problème calcul de moment intérieur 31-10-20 à 15:29

Ils imposent une méthode comme ça c'est plus facile à corriger lorsqu'on leur rend les copies disent les enseignants.

Du coup ici, je regarde à droite de la coupure (sur BC).

Il manque une borne d'intégration car j'ai posé que ça valait 0 car la distance entre M et C vaut 2L - x.

Normalement l'erreur ne provient pas de mon produit vectoriel car je retrouve bien le premier terme de la correction c'est à dire F(2L-x). Je me suis dit que si je change le signe de MC alors tout était faux même le premier terme. (avec \vec{MC} = (2L-x)\vec{x} )

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 31-10-20 à 19:00

J'ai un souci avec ton calcul : il ne fait intervenir aucun vecteur !

Comment tu arrives à t'y retrouver pour faire le produit vectoriel ?

\textcolor{red}{\vec{M}} = \textcolor{red}{\vec{MC}} \wedge \textcolor{red}{\vec{T}}

J'ai compris ton erreur : tu me dis que tu considères ce qui se passe à droite de la coupure, or ta borne d'intégration considère l'ensemble de la poutre, ce qui n'est pas correct. Elle ne doit considérer que la portion à droite de la coupure.

Posté par
Newdayre : Problème calcul de moment intérieur 31-10-20 à 19:32

Oui j'ai pas fait intervenir les vecteurs, c'est vrai, je les ai déjà dans mon torseur sur le schéma car je sais que \vec{M} = \vec{MC} \wedge \vec{T} = M(x) \vec{z}   et je cherche M(x), je sais que ce n'est pas rigoureux mais je ne voulais pas surcharger mes calculs et que ça reste un minimum lisible...

C'est vrai que mes  bornes d'intégration sont douteuses, mais je ne sais pas vraiment quoi mettre d'autres. Pour vérifier que mes bornes étaient "correctes" j'ai fait le calcul de T(x) et je suis retomber sur la réponse mais pour le calcul du moment M(x)ça ne marche pas

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 01-11-20 à 11:58

Bonjour Newday,

Désolé pour le temps de latence, nous sommes en plein dans le pic d'activités traditionnel des , je dois jongler entre les 3 sites.

Je vais me faire violence en isolant un des tronçons avec ta méthode calculatoire. Je te poste ça d'ici peu

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 01-11-20 à 13:24

Je vais isoler un tronçon x [AB] (effort réparti représenté en rose) :

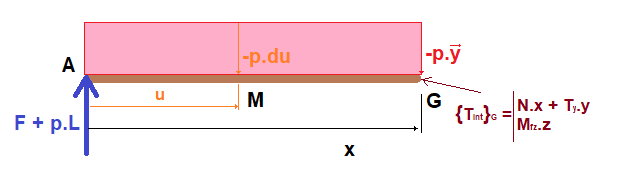
Problème calcul de moment intérieur

Equation de la résultante par rapport à \vec{x} :

N(x) = 0

Equation de la résultante par rapport à \vec{y} :

T_y - \int_{0}^{x} p.du + F + p.L = 0

Equation de moment en G par rapport à \vec{z}

\vec{z}.(\vec{GA} \wedge (F + p.L).\vec{y}) + \vec{z}. \int_{0}^{x} (\vec{GM} \wedge -p.du.\vec{y}) + M_{fz} = 0

\Leftrightarrow -(F + p.L).x + \vec{z}.\int_{0}^{x}(u - x).\vec{x} \wedge (-p.du.\vec{y}) + M_{fz} = 0

\Leftrightarrow -(F + p.L).x - p.\int_{0}^{x}(u-x).du + M_{fz} = 0

\Leftrightarrow M_{fz} = +(F + p.L).x + p.\big[\dfrac{(u-x)^2}{2}\big]^x _0 = 0

\Leftrightarrow M_{fz} = +(F + p.L).x - p.\dfrac{x^2}{2} = 0

Posté par
Newdayre : Problème calcul de moment intérieur 01-11-20 à 18:26

Bonjour,

Pas de soucis pour le temps de retard, et merci pour votre réponse et tout le temps que vous m'avez accordé. Après m'avoir arraché les cheveux,mon erreur venait finalement bien de mes bornes d'intégrations:  

il fallait que je fasse le calcul avec p(x)= \int_{x}^{2L}{pdx} et non pas p(x)= \int_{}^{2L-x}{pdx}

Posté par
gbm Webmasterre : Problème calcul de moment intérieur 01-11-20 à 18:56

Oui c'est ce que je sous-entendais dans mon message du 31-10-20 à 19:00 quand j'écrivais :

Citation :
J'ai compris ton erreur : tu me dis que tu considères ce qui se passe à droite de la coupure, or ta borne d'intégration considère l'ensemble de la poutre, ce qui n'est pas correct. Elle ne doit considérer que la portion à droite de la coupure.

Ce qui correspondait bien, dans ton cas, à la portion de poutre entre la coupure d'abscisse x et 2L.

C'est d'ailleurs la raison pour laquelle j'ai traité l'autre portion de la poutre à étudier.

Je t'en prie pour l'aide, bonne soirée et à une prochaine fois !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !