Inscription / Connexion Nouveau Sujet
Principe de Fermat
Bonjour à tous,
Je viens à vous pour vous demander une petite explication à propos d'une formule concernant le principe de Fermat :
L =  n.dl
n.dl  L = n1.AI + n2.IB
L = n1.AI + n2.IB
(Avec A dans un milieu de réfringence n1 et B dans un autre milieu de réfringence n2. Ces 2 milieux sont donc séparés pas un interface sur lequel se trouve I, mais I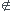 [AB])
[AB])
Ce que je ne comprend pas, c'est à quelle distance correspond ce L ? (Ça ne semble pas être AI+IB puisque n1AI + n2IB  AI + IB pas définition)
AI + IB pas définition)
Alors quelle est cette distance L ? On la voit où ?
Merci 
Bonjour Taupinaz,
pas de probleme :
On considere un rayon lumineux se deplacant dans le milieu 1 avec la vitesse v1 et parcourant la distance AI. La duree de ce parcours est t1 = AI/v1.
Ce rayon, apres etre passe par I, se trouve sans le milieu 2 et parcourt la distance IB a la vitesse v2 : la duree de ce 2ieme parcours est t2 = IB/v2. Pour aller de A a B ce rayon a donc mis le temps t = t1 + t2.
Imagine maintenant un autre rayon lumineux se deplacant dans le vide, donc a la vitesse c. Quelle distance parcourt-t-il pendant le temps t precedent ? C'est bien sur D = ct = c(AI/v1 + IB/v2), ou encore n1AI + n2IB, par definition des indices de refraction.
Tu reconnais dans cette distance D le chemin optique L ? Eh bien voila son interpretation :
Le chemin optique L suivi la la lumiere pour aller d'un point A a un point B en traversant des milieux d'indices differents est mesuré par la distance L qu'il parcourerait dans le vide a la vitesse c.
OK ?
Bon week-end et a une prochaine fois. Prbebo.
Mais ça fausse la distance AI + IB si on remplace v1 et v2 par c ?! D sera bien plus court selon le calcul que dans la réalité, non ?!
Bonjour Taupinaz,
je crois que tu n'as pas bien compris : je n'ai jamais dit que la lumiere devait parcourir a la vitesse c la distance AI + IB. J'ai simplement parle de la distance qu'elle parcourerait (note le subjonctif) dans le vide, donc en ligne droite et a la vitesse c : cete distance est egale a L d'apres ma demonstration.
Je vais appuyer avec un exemple simple : suppose que la lumiere, au lieu de se deplacer dans le vide a la vitesse de 300000 km/s, se deplace a ... 3 m/s. On prend pour le milieu a un indice de refraction n1 = 1, cad que la lumiere dans le milieu 1 de deplace aussi a 3 m/s, et on choisit pour le milieu 2 un indice n2 = 1.5, cad que la lumiere s'y deplace a la vitesse v2 = 3/n2 = 2 m/s (en d'autres termes je respecte la definition de l'indice de refraction n = c/v, mais j'ai modifie - severement- la valeur numerique de c).
On prend dans le milieu 1 un trajet AI = 6 m, et dans le milieu 2 un trajet IB = 4 m. Quel est le chemin optique L = n1.AI + n2.IB ? C'est L = 1 x 6m + 1.5 x 4 m = 12 m.
Maintenant, quel temps met le "rayon lumineux" pour parcourir le chemin A -> I -> B, avec les vitesses v1 et v2 ? C'est t = t1 + t2, avec t1 = 2 s (6 m parcourus a 3 m/s) et t2 = 2 s (4 m parcourus a 2 m/s), soit t = 4 s.
Et enfin, quelle distance D parcourt la "lumiere" dans le vide pendant ce temps ? facile : 3 m/s pendant 4 s ca fait 12 m... exactement la valeur de L. Mais je n'ai jamais dit que cette distance C etait egale a AB, ni a AI + IB ! Elle est forcement plus grande.
Je t'invite donc a relire la phrase soulignee dans mon precedent post...
A bientot, Prbebo.



