Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Pression tube

Posté par
azerty4 16-12-19 à 17:41

Bonjour,

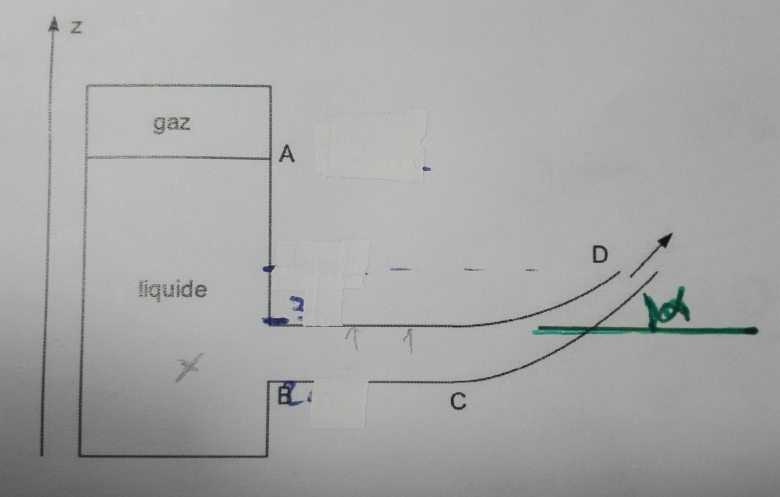
on s'intéresse à à la force exercée sur fluide sur le tube (BCD)
Pour cela on dispose :
• Des altitudes za zb zc
• De la pression du gaz pi et de la pression atmosphérique de sortie en D patm
• De l'angle que fait le tube de sortie (CD) avec l'hozitontale
• Des rayons rB = rC et rD
• De la masse totale de fluide contenue dans le tube m
• De la masse volumique

On suppose le fluide parfait et incompressible

Voici mon raisonnement :

- Appliquer le bilan de qdm \int \int \rho \vec u (\vec u . \vec n) dS = \int \int - p \vec n dS + \int \int \int \rho \vec g dV et projeter

J'ai décomposé la surface en 3 parties :
- La section de sortie SD
- La section d'entrée SB
- Le contour, paroir du tube

Je bloque pour l'application du théorème, voici mes questions le rayon d'entrée RB = rC = 1m ce qui est 'grand'
-La pression à l'entrée PB  n'est pas uniforme, elle dépend de l'altitude

-Peut on considérer que UB vitesse d'entrée est constante selon z .
- Considérer une pression qui dépend de z (P = Pi + g (zA - z)) ) et ajouter la masse m du fluide ne revient pas a prendre en compte 2 fois le poids ?

Nous n'avons fait en cours  que des écoulement horizontaux où la gravité n'intervient pas

Merci d'avance pour votre aide

Bonne soirée

Pression tube

Posté par
vanoisere : Pression tube 16-12-19 à 19:41

Bonjour
Je pense que tu te compliques la vie avec tes intégrales triples !
En raisonnant sur la conservation du débit de liquide et la relation de Bernouilli, tu peux obtenir l'expression de la vitesse en B. Pour la résultante des forces, tu peux t'inspirer de ce document :

Posté par
vanoisere : Pression tube 16-12-19 à 19:53

Je me suis mal relu. Il faut lire : "tu peux obtenir l'expression de la vitesse en D"
La vitesse en B n'est pas à déterminer pour résoudre le problème.

Posté par
azerty4re : Pression tube 16-12-19 à 20:18

Bonjour,

j'ai effectivement trouvé la vitesse en D avec Bernouilli et conservation du débit

Cependant dans l'exemple présenté sur le site, le poids du fluide est négligé
On trouve \vec F = ( - \rho u_B ^2 S_B + \rho u_D ^2 S_Dcos(\alpha ) + P_B S_B - P_D S_B) \vec u_x + ( \rho u_D ^2 S_D sin (\alpha -mg ) \vec u_y

Cela revient a considérer PB constante sur toute la section de rayon 1m ?


Je suis un peu perdu

Merci d'avance pour votre aide

Posté par
azerty4re : Pression tube 16-12-19 à 20:30

Correction de mon message :
Petite erreur pour la pression en D :
\vec F = ( - \rho u_B ^2 S_B + \rho u_D ^2 S_Dcos(\alpha ) + P_B S_B - P_D S_B cos(\alpha )) \vec u_x + ( \rho u_D ^2 S_D sin (\alpha) - P_D S_B sin(\alpha ) -mg ) \vec u_y

Posté par
vanoisere : Pression tube 16-12-19 à 21:15

Pour la pression en B :
Que vaut la différence d'altitude entre A et le milieu de l'ouverture b ? Je pense qu'elle est suffisamment grande devant R  pour traiter le problème comme si la pression était la même en tout point d'une section droite de canalisation.  Tu peux aussi appliquer Bernouilli entre A et B.

Posté par
azerty4re : Pression tube 16-12-19 à 21:31

La différence entre A et le milieu de l'ouverture en B vaut 7m
Le diamètre de l'ouverture est de 2 mètres

Posté par
vanoisere : Pression tube 16-12-19 à 21:41

Je pense que l'approximation peut se faire.  L'erreur dans la partie haute de la canalisation est assez bien compensée par l'erreur de signe opposée dans la partie basse. De toutes les façons, à ce niveau d'avancement dans le programme, je ne vois pas quoi faire d'autre.

Posté par
azerty4re : Pression tube 16-12-19 à 21:45

D'accord merci
Donc l'expression du bilan est force vous semble correcte ?
Plus qu'à remplacer les pressions et vitesses avec Bernouilli et conservation du débit
Merci pour votre aide

Posté par
vanoisere : Pression tube 16-12-19 à 22:26

Citation :
Donc l'expression du bilan est force vous semble correcte ?

j'ai un problème pour vérifier les signes de ta formule. Tu as sûrement commis une erreur de copie :
Citation :
on s'intéresse à à la force exercée sur fluide sur le tube

S'agit-il de la force exercée par le fluide sur le tube (cas de mon document) ou de la force exercée sur le fluide par le tube ?
Principe des actions réciproques : il s'agit de deux forces opposées...

Posté par
azerty4re : Pression tube 16-12-19 à 22:40

Effectivement, l'expression que j'ai fournie a une erreur de signe
On nous demande la force exercée par le fluide sur le tube
Il faut donc multiplier l'équation par -1 a droite

Sinon cela semble correct ?
Intégrer la pression avec la relation hydrostatique sur la surface aurait été possible pour le pas considérer la pression constante en B ?

Merci d'avance

Bonne soirée

Posté par
vanoisere : Pression tube 16-12-19 à 23:10

Raisonner en statique sans considérer la pression uniforme dans une section droite introduirait une erreur importante car cela négligerait l'influence de la variation d'énergie cinétique massique dont tient compte Bernouilli.
Comme sur le document que je t'ai fourni, il faut donc considérer que le fluide est soumis à la force -\vec{F}
En notant Dm le débit massique :
Dm=.SA.VA=.SB.VB = .SD.VD :

D_{m}.\left(\overrightarrow{V_{D}}-\overrightarrow{V_{B}}\right)=D_{m}.\left[V_{D}.\left[\cos\left(\alpha\right).\overrightarrow{u_{x}}+\sin\left(\alpha\right).\overrightarrow{u_{y}}\right]-V_{B}.\overrightarrow{u_{x}}\right]-\overrightarrow{F}-m.g.\overrightarrow{u_{y}}+P_{B}.S_{B}.\overrightarrow{u_{x}}-P_{atm}.S_{D}.\left[\cos\left(\alpha\right).\overrightarrow{u_{x}}+\sin\left(\alpha\right).\overrightarrow{u_{y}}\right]

\overrightarrow{u_{x}} : vecteur unitaire horizontal orienté vers la droite ;

\overrightarrow{u_{y}} : vecteur unitaire vertical orienté vers le haut .

Posté par
azerty4re : Pression tube 17-12-19 à 18:10

Bonsoir

Merci beaucoup pour votre aide c'est beaucoup plus clair

J'obtiens le même résultat avec notre méthode d'intégrales doubles et triples ( nous sommes obligé d'utiliser ça et pas autre chose)

Je pense que le - devant le vecteur F est un = dans la formule et F représente la force exercée sur le fluide c'est ça ?

Merci encore

Belle soirée !

Posté par
vanoisere : Pression tube 17-12-19 à 19:05

Citation :
Je pense que le - devant le vecteur F est un = dans la formule et F représente la force exercée sur le fluide c'est ça ?

Je ne comprends pas bien ta question. Volontairement, je n'ai pas simplifié la formule que je t'ai fournie pour mieux en montrer le sens physique. Le système étudié est le liquide contenu à la date t dans le tube. La variation par unité de temps de sa quantité de mouvement D_{m}.\left(\overrightarrow{V_{D}}-\overrightarrow{V_{B}}\right) est égale à la somme des forces exercées sur le liquide par le milieu extérieur. Si \overrightarrow{F} désigne la force exercée par le liquide sur le tube, le principe des actions réciproques (action et réaction) permet d'affirmer que la force à prendre en compte dans la formule (force exercée par le tube sur le liquide) est (-\overrightarrow{F}) .


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !