Bonjour,

Pourrais-tu faire un schéma de la situation, exprimer littéralement l'effort tranchant et le moment fléchissant (repère à définir) puis dérouler ton raisonnement pour le calcul de la flèche (formule, conditions aux limites, ...) ?

Bonjour,

Ok d'accord.

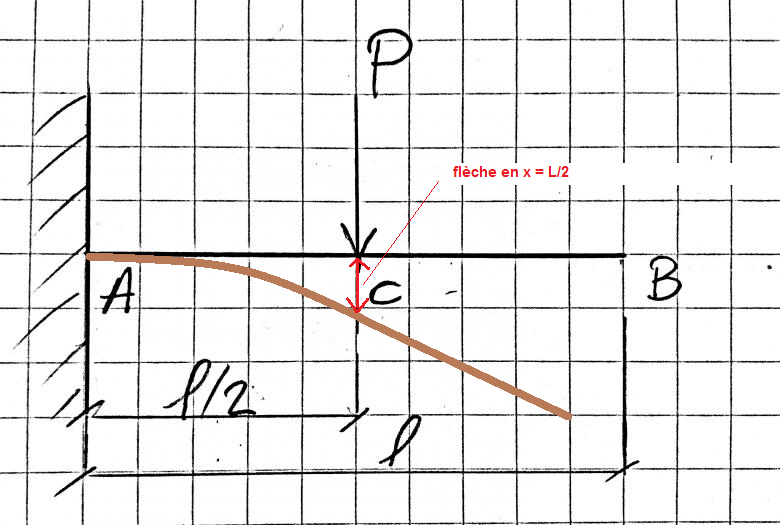
On va considère une console AB de longueur supposée  non pesante, supportant, en son milieu C, une charge concentrée d'intensité P.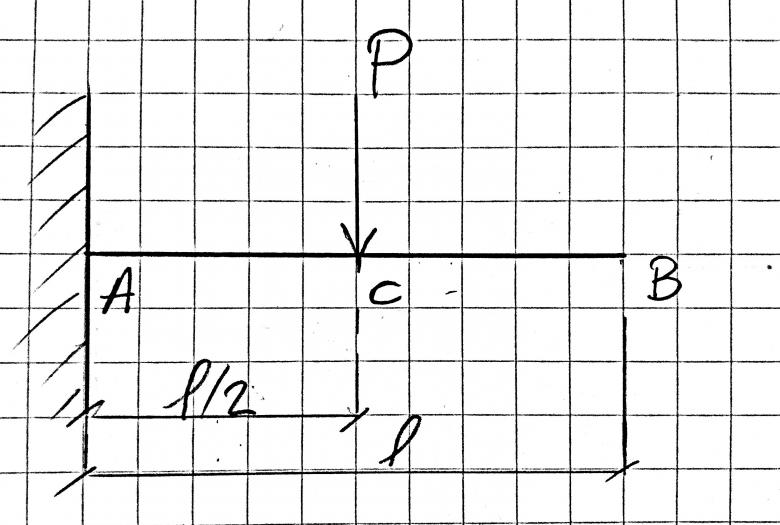



xF x = 0, ?F y = 0, M A = 0 .

?F x = 0:    H A = 0
F y = 0:    RA - P  = 0;
M A = 0:    M A - l/2 * P  = 0;

H A = 0
R A = P
M A = l/2 * P

Vérification
- l * R A + M A + l/2 * P  = 0

Tronçon : 0 ? 1 <l/2

L'effort tranchant :

T(x) = + RA

Le moment fléchissant

M (x ) = + R A * (x ) - M A

Tronçon : /2 ? x <l

L'effort tranchant :

T (x ) = + R A - P

Le moment fléchissant

M (x ) = + R A * (x) - M A - P  * (x - l/2)

Pour la flèche je ne sais pas.

Par contre je connais équation de la déformée quand la  charge concentrée est à l' extrémité.

Alors, pour commencer, quelques rappels du cours :

______________________________________________________

Pour tracer les diagrammes des efforts pour une poutre soumise à un effort concentré et/ou à un champ linéique, on imagine qu'une section droite S de centre de gravité G et d'abscisse x (repère défini) établit une coupure fictive en x de la poutre :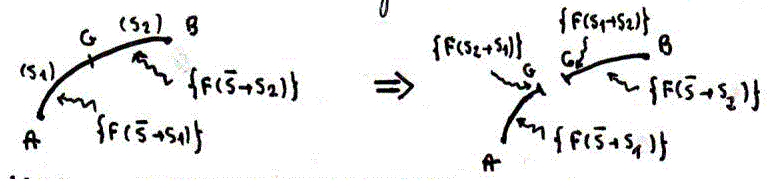



Par définition, le torseur de cohésion (ou torseur des efforts intérieurs) s'écrit :



Si tu appliques le principe fondamental de la statique, on démontre que ce torseur des efforts intérieurs peut s'écrire en un torseur des efforts extérieurs appliqués à la section ou , au signe près :

("+" ce qui est à droite)

("-" ce qui est à gauche)

Voilà pourquoi tu peux analyser une poutre à gauche ou à droite de la section droite d'abscisse x (au signe près) pour tracer des diagrammes d'efforts intérieurs ou encore pour calculer ce torseur.

______________________________________________________

La première remarque que je peux faire, tu n'as pas défini le repère choisi sur ton schéma => sans cela, tes notations et calculs n'ont pas de sens.

Repère (A,x,y,z) avec (Ax) l'axe des abscisses et (Ay) l'axe des ordonnées :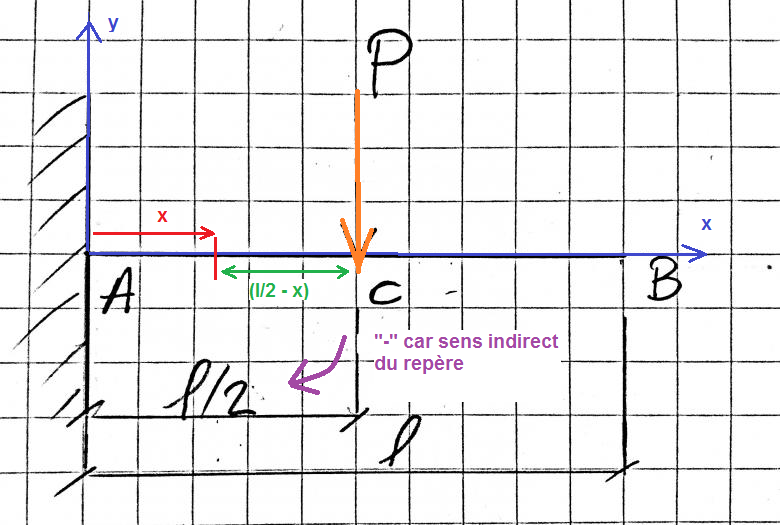



Diagramme de l'effort tranchant Ty :

* x compris entre l/2 et l :

Ty = +0 (je regarde les efforts à droite) ;

* x compris entre 0 et l/2 :

Ty = -P

=> le tracé du diagramme de l'effort tranchant est facile.

Diagramme du moment fléchissant par rapport à (Az) Mfz :

* x compris entre l/2 et l :

Mfz = 0 ;

* x compris entre 0 et l/2 :

Moment = effort x bras de levier au signe près (négatif car le moment déplace la poutre dans le sens indirect du repère)

Mfz = -P*(l/2 - x)

=> le tracé du diagramme du moment fléchissant est facile.

Détermination de la flèche de la poutre :

Tu as très certainement vue en cours l'expression du déplacement de la poutre soumise à une flexion, en fonction du moment fléchissant :



Pour déterminer le déplacement u(x) il faut donc faire une double intégration puis déterminer les constantes d'intégration en fonction des conditions aux limites (par exemple au niveau de l'encastrement, continuité de la fonction déplacement, etc.).

Bon je vous remercie beaucoup pour toutes les informations.

Mais je sais que j'ai pas besoin de tout ça pour répondre à ma question qui est « Donner la flèche en tout section "  pour se schéma, que je vous ai transmis tout à l'heure est-ce que vous pouvez me m'aider ? Sans utiliser le torseur de cohésion

Or, juste pour info si jamais tu souhaites retrouver la valeur indiquée (troisième cas) :

Cf. ici pour ton cas (partie "Poutre encastrée") :

avec a = L/2

Ha génial !!! Je vous remercie mille fois !

De rien !

A une prochaine fois peut-être !

Bonjour,

J'ai une question pour le même sujet.

je n'arrive pas à faire l'équation pour trouver sa ""

Krk

Bonjour,

Je ne comprends pas d'où vient cette expression, ce n'est pas homogène à une flèche :



avec

etc.

Je me disais aussi, il y a un truc louche.

Car après ont me demande de tracez la lignes déformée correspondante à échelles :

l = 8 cm

= 1cm


krk

La question précédente nous demande : En supposant la console d'inertie constante I, donnez la flèche en toute section située à la distance x de A .

je suis perdu...là

Pouvez- vous m'aider svp ?

Bonsoir,

Mon schéma n'est pas à l'échelle, mais la déformée en fonction de x aura cette allure :

Ok d'accord pour le schéma, pour la question précédente il me demande : En supposant la console d'inertie constante I, donnez la flèche en toute section située à la distance x de A .

Selon vous je dois utiliser l' équation suivante :




krk

C'est la raison pour laquelle je voulais que tu détermines l'équation de la déformée en fonction de x depuis le début

Pour rappel, je t'ai donné un lien qui peux t'aider à démontrer cette équation.

Attention, il faut utiliser la formule générale, fonction de x pour faire le tracé ! Mais tu peux t'aider de points particulier (x = 0, x = L/2).

Bonjour,

Je suis en train de faire l'équation avec les primitives, mais je suis bloqué au niveau des constante.

L'équation différentielle :












Je n'arrive pas à déterminer les deux constantes...

Je procédé comment pour les déterminer ?

Bonjour,

C'est expliqué dans le premier lien fourni dans mon message du 01-11-18 à 15:47

Ça m'a aider pour le début, mais pour les constante je n'ai pas compris.

S'il vous plaît un petit indice

Le calcul des constantes K se fait en choisissant des conditions aux limites de zones:

En A :

x = L/2

Il faudrait que vous m'aider, s'il vous plaît.

Je suis en train de me tires les cheveux ! Je suis complètement perdu la !

A l'encastrement, il n'y a pas de déplacement, donc

y(0) = 0
y'(0) = 0

Oui je sais .

Je fait comment pour déterminer K ? ? C'est ma question

K1 =

K2 = 0

Equation de la déformée pour x compris entre 0 et L/2 :



Remarque : je reprends mon expression du moment fléchissant trouvée dans mon message du 01-11-18 à 14:58.



Conditions aux limites :

- à l'encastrement :



soit pour x [0 ; L/2] :



Sauf faute d'inattention

***Message corrigé***

Ok d'accord !! Je vous remercie.

Ma flèche correspond à :



??

Bien vu ! J'ai fait une faute d'inattention, j'ai corrigé mon message précédent

C'est l'équation de la déformée y en fonction de l'abscisse x de la poutre.

On parle souvent de flèche pour désigner l'abscisse à laquelle le déplacement est maximal.

Attention à ne pas confondre les deux termes

Je vous remercie mille fois !!

Une derrière question ou je peu trouve un cours complet sur l' équation de Clapeyron. ?

Par exemple ici : (§3.1.1).

Je t'en prie ! Je te souhaite un bon dimanche et une bonne reprise.

Merci bon dimanche à vous aussi.