Inscription / Connexion Nouveau Sujet
Pour passer le temps... si on veut.
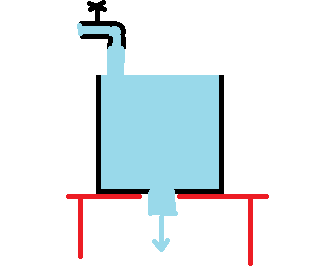
On a un bac parallélépipédique de hauteur 1 m et de surface de base = 1 m² posé sur une surface horizontale.
Le bac est plein d'eau à ras bord.
Simultanément, à l'instant t = 0, on ouvre un robinet qui débite 1,5 L/min dans le bac et on ouvre une bonde dans le fond du bac.
A l'instant t = 0, le débit à travers la bonde est de 2 L/min.
Question : Quel temps faudra-t-il pour que le réservoir soit vide ?
-----
Attention, c'est un problème de Physique et il faut en tenir compte.
Blanker vos réponses SVP.

Salut J_P,
Ca faisait longtemps qu'on n'avait pas eu un petit moment sympathique sur l'île  .
.
J'attends un peu avant de poster une solution, au risque de finir par faire cette détente qu'entre correcteurs 
Salut gbm
Oui, pas beaucoup d'amateurs.
Je finirai par penser que dès que le mot "Physique" se trouve dans un énoncé, beaucoup réchignent... Dommage. 
Bonjour J.P
En lisant ta solution de la baignoire qui fuit...,
J'ai relevé une erreur dans ta conclusion:
Le temps mis pour vider le bac est donc infini.
Mais ce qui m'a intéressé, c'est la quantité d'eau que l'on doit déverser jusqu'au moment ou le niveau se stabilise .
Quelle est cette quantité?
Merci pour cet exercice.
Bonjour à tous
Volume d'eau E versé dans le récipient pour atteindre le niveau stable.
On appelle T le temps correspondant au volume demandé
La section de la bonde S = 2*10-3)/(60 * √(2g) 7.53 mm²
7.53 mm²
a = -S√(2g) =- 10 -4)/3 m3/s débit de la bonde ; D = 2.5 * 10-5 m3 / s débit du robinet ; D²/a² = 0.5625 et g = 9.81 m/s².
On demande E = D*T
Calcul de T
A l'instant t La hauteur du niveau de l'eau est h(t), Le débit de la bonde Q(t) = S√(2gh(t)) (théorème de Torricelli)
Si le volume d'eau est V(t) = h(t)*1 = h(t), dV = dh = (D-Q(t))dt.
Donc dh = (D - S√(2gh(t))dt= (D+a√h) dt.
On considère h  [1 ; D²/a²[ et t
[1 ; D²/a²[ et t  [0 ; +
[0 ; + [, avec (D + a √h)
[, avec (D + a √h)  0 et dt= dh/(D+a√h).
0 et dt= dh/(D+a√h).
A l'instant t = T, la hauteur du niveau est h = H tel que :
l'intégrale dt = T =
.
La fonction f : h
admet sur [1 ; D²/a² [ une primitive F(h) = 2/a² (a(√h -1) - D *ln |
),
qui donne : T = 2/a² (a(√H -1) - D*ln||).
Quand H  D²/a², |(a√H +D)/(a+D)|
D²/a², |(a√H +D)/(a+D)| 0 , ln |(a√H +D)/(a+D)|
0 , ln |(a√H +D)/(a+D)| -
- et T vers +
et T vers + .
.
En conséquence, le niveau stable à 0.5625 m n'est jamais atteint en temps fini .
Par exemple le niveau 0.562 500 001 à 10-9 de la limite théorique 0.562 5 n'est atteinte qu'au bout de 10j 12h 16min environ après une dépense de 22,700 m3 d'eau !
De plus le diamètre de la bonde n'est que de 3,1 mm. Etonnant non ?
Enfin, la réponse à la question est : une quantité d'eau illimité de sorte que toute l'eau de l'univers ne serait pas suffisante !
Remarque : on a supposé que l'eau est un liquide parfait, les frottements sont négligeables et le régime est laminaire (pas de turbulence)
ming0,
Je ne vois rien de "répréhensible" à écrire "Le temps mis pour vider le bac est donc infini.".
L'infini n'est pas un nombre, cette phrase est tout simplement équivalente à "Le bac ne sera jamais vide"

Bonsoir JP
Je veux bien t'accorder cette interprétation de la notion d'infini qui est de l'ordre des mathématiques.
Cependant il est plus judicieux de montrer que dans les conditions (parfaites) indiquées ci-dessus non seulement le bac ne serait jamais vide mais le calcul théorique est une limite jamais atteinte déjà.
Tu écris: "lorsque la hauteur d'eau dans le bac sera de 0,5625m..." Ce qui est erroné(mathématiquement).
Cela dit, j'ai bien aimé ce problème et le t'en remercie

 Cliquez pour afficher
Cliquez pour afficher
