Inscription / Connexion Nouveau Sujet
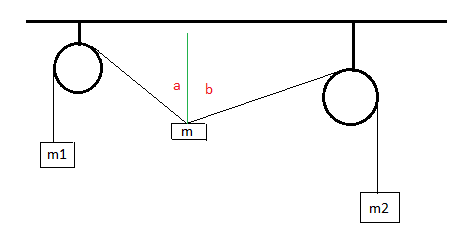
Poulies et masses
Salut à tous,
J'ai un exo de mécanique où je dois déterminer les deux angles a et b formés entre les cordes des deux poulies et la verticale.
Alors quand je fais l'inventaire des forces :
suivant un axe oZ dirigé vers le bas
poids de m1 : Pm1 = m1.g
tension de la corde pour m1 : T1
poids de m : Pm = m.g
tension des cordes pour m, T'1 coté a et T'2 coté b
poids de m2 : Pm2 = m2.g
tension de la corde pour m2 : T2
on précise que le système est immobile, on néglige le poids de la poulie et des cordes.
Donc vu que le système est immobile, la somme des forces verticales et la somme des forces horizontales est nulle (principe d'inertie) :
 Fh = 0
Fh = 0
 Fv = 0
Fv = 0
Donc si on décompose les deux vecteurs tension situés de part et d'autre de m, on a suivant un axe oX orienté vers la droite :
-T'1x + T'2x = 0
Comme les poids et les tensions se compensent pour m1 et m2 alors on obtient :
T'1y + T'2y + m.g = 0
Et là je sais pas comment faire pour remonter à l'angle a, et déduire b.
comment évaluer les tensions coté a et coté b ? que valent elles ? et comment remonter aux angles ensuite ?
Merci
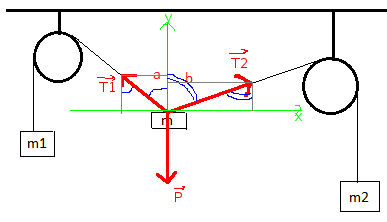
Bonjour,
Oui, je suis d'accord avec vous... Mais si vous aviez commencé par représenter les vecteurs-forces sur votre schéma, vous auriez sûrement trouvé, par projection/trigonométrie, que :
T1x = T1.sin(a)
T1y = T1.cos(a)
T2x = T2.sin(b)
T2y = T2.cos(b)
Maintenant, comme les fils sont tendus et qu'on néglige leur poids tout comme celui de la poulie (donc pas d'inertie sur la poulie), alors les tensions se "propagent" le long de chaque fil.
Ainsi, par le principe d'inertie appliqué à chaque masse (m1) et (m2).
T1 = P1 = m1.g
T2 = P2 = m2.g
Maintenant, à vous de voir comment vous pouvez vous en sortir avec cela pour en exprimer les angles (a) et (b) 
Sur ce schéma, je n'ai pas représenté les projetés [i](pour ne pas l'alourdir) mais je suppose que vous voyez où ils se situent !  [/i]
[/i]
Merci.
J'avais déjà fait les projections, j'avais trouvé ces relations, c'est justement à partir de ces relations que je n'arrive pas à exprimer les angles.
J'ai ajouté T1x + T1y = T1 = m1.g = T1(sin a + cos a) etc.
Mais je ne trouve rien qui me permette de trouver a..
Si vous écrivez que T1 = T1x + T1y sous cette forme dite scalaire (et non vectorielle), c'est faux.
C'est de part le théorème de Pythagore.
Sûrement...
Ceci dit, désolé, je ne suis pas très à l'aise avec des systèmes d'équations à 2 inconnues du genre trigonométrique :
m1.sin(a) - m2.sin(b) = 0
m1.cos(a) + m2.cos(b) = m
Mais je cherche... Ou alors, quelqu'un de plus calé que moi en maths saura mieux te répondre... Il reste aussi le forum de maths au besoin ! 
Votre texte est-il complet ?
Bonne remarque...
J'ai quand même bibouillé un truc (maintenant, je ne puis te garantir ce que cela vaut... Je ne suis pas prof. de maths !
 )
)
Changement de variable :
Je pose
et
Donc j'ai une première équation qui découle de ma relation n°2 : X+Y=1
Formulaire de trigo :
J'élève au carré la première relation m1.sin(a) = m2.sin(b) et j'utilise le fait que sin² = 1 - cos² pour la transformer en cos²
m1²(1 - cos²a) = m2²(1-cos²b)
J'ai développé
m1² - m1².cos²(a) = m2² - m2².cos²(b)
J'ai opéré mon changement de variables donc...
m1² - (m.X)² = m2² - (m.Y)²
Du coup, j'arrive à cette relation : X² - Y² =
Et comme je peux factoriser X² - Y² = (X+Y)(X-Y) (avec n'oublions pas que X+Y=1)
Système à résoudre :
X + Y = 1
X - Y =
Je pose K =
X = (1-K)/2
Y = (1+K)/2
D'où l'expression de cos(a) et de cos(b) par changement de variable inverse...
cos(a) =
cos(b) =
- sauf erreur de ma part -
Ah oui Heroes31, système trigonométrique c'est la première fois que j'en voyais !
Ta méthode par changement de variable marche puisque c'est le resultat attendu dans l'indication de résultat.
Je vais reprendre ta méthode pas à pas et essayer de refaire moi meme, merci beaucoup ! 
Une dernière précision :
Pourquoi on a un moins ici :
m1.sin(a) - m2.sin(b) = 0
Alors que m1.sin(a) = T1x 1)
et : m2.sin(b) = T2
x
Mais avec ton axe Ox orienté vers la droite, c'est le terme 1) qui doit avoir le signe moins, non ?
Une dernière précision :
Pourquoi on a un moins ici :
m1.sin(a) - m2.sin(b) = 0
Alors que m1.sin(a) = T1x 1)
et : m2.sin(b) = T2x 2)
Mais avec ton axe Ox orienté vers la droite, c'est le terme 1) qui doit avoir le signe moins, non ?
m1.sin(a) - m2.sin(b) = 0
Si j'applique la RFD :
En projetant sur l'axe (Ox) que j'ai donc mis de manière habituelle :
0 - T1x + T2x = 0 d'où T1x = T2x
D'où m1.sin(a) = m2.sin(b) (après simplification)
Ce qui donne, après transposition, m1.sin(a) - m2.sin(b) = 0 = -m1.sin(a) + m2.sin(b)
Donc on a bien écrit la même chose !

je pense que :
X = (1+K)/2
Y = (1-K)/2
Non ?
Oui, c'est ce que j'ai marqué...
Ta méthode par changement de variable marche puisque c'est le resultat attendu dans l'indication de résultat.
Super si c'est bien le résultat attendu... C'était pour ainsi dire une méthode (souvenir de MathsSup.) que je connaisse afin de s'affranchir des cos et des sin.
Après, faut voir comment ton prof va procéder... étant donné que le changement de variable, c'est élégant !
Mais le reste, c'est purement calculatoire et on ne sait pas toujours vers quoi on tend...
Pour ma part, entre 10h et 12h (entre-coupé du taff à faire aussi), j'ai du recommencer trois fois pour me dépatouiller et sortir un truc, après avoir essayer 3 autres changements de variables (mais dans le même style X = f(cos...) )
Je vais reprendre ta méthode pas à pas et essayer de refaire moi meme, merci beaucoup !
Oui, c'est le mieux étant donné que je n'ai pas détaillé tous les calculs... A ton service !
Super si c'est bien le résultat attendu... C'était pour ainsi dire une méthode (souvenir de MathsSup.) que je connaisse afin de s'affranchir des cos et des sin.
Après, faut voir comment ton prof va procéder... étant donné que le changement de variable, c'est élégant !
Mais le reste, c'est purement calculatoire et on ne sait pas toujours vers quoi on tend...
Perso je planche dessus depuis hier soir, et même avec toutes les formules d'addition, multiplication en trigo, j'ai rien sorti de tel... Donc le changement de variable va peut être s'imposer. C'est peut être le but de l'exo, je verrai =)
Super sympa à toi, à une prochaine

Bonsoir,
Les équations de projection nous donnent deux équations. Il y a deux inconnues, les angles a et b donc une solution.
La recherche de a et b par Héorès31 est bien sûr correcte .
En réfléchissant, j'ai utilisé le fait que le polygone dynamique formé par les trois forces P, T1 et T2 est fermé.
On a donc un triangle formé par ces trois forces.
En divisant par g on obtient un triangle dont les trois côtés sont les masses m, m1 et m2.
Or dans un triangle quelconque la trigonométrie nous donne de nombreuses relations dont :
a^2 = b^2 +c^2 - 2bc*cos et les deux autres.
A utiliser dans notre triangle. JED.
Ah ouais !
Bien vu pour la relation d'Al-Kashi (Pythagore généralisé). Il ne me serait pas venu une telle idée...
C'est très élégant !
Par contre, il faut préciser que dans son cas à IronMetal, l'angle A, c'est a pour son exo.
Et que ton a, b, c, c'est les longueurs des forces T1, T2 et P, opposés aux angles... 
Plutôt joli oui =)
Mais :
En réfléchissant, j'ai utilisé le fait que le polygone dynamique formé par les trois forces P, T1 et T2 est fermé.
Bonsoir,
Bien sûr la solution proposée n'est valable que dans le cas d'un solide en équilibre.
Rappel :
Quand un solide soumis à trois forces non parallèles est en équilibre :
- les trois forces sont coplanaires.
- les trois forces sont concourantes.
-La somme vectorielle des trois forces se réduit au vecteur nul.
Cette dernière proposition nous conduit à une solution analytique (projections) ou à une solution graphique (polygone dynamique
fermé).
Vous qui avez la chance de faire des études dans ce domaine, profitez en ,c'est vraiment intéressant. Si vous avez quelques minutes
donnez nous en quelques mots la solution proposée par votre enseignant(e).
Merci d'avance. JED.


