Inscription / Connexion Nouveau Sujet
poulie et ressort
Bonjour
1-on me demande de trouver une relation entre x2'',x2 ,x1 ,m2 ,g, k. en appliquant le PFD a M2, j'obtiens ainsi l'equation x2 '' = g-k/m2(AM2 -l0) et j'ai du mal a ecrire AM2 en fonction de x1 et x2 ( je ne pense pas que c'est x2-x1) vu qu'ils sont definis par rapport a O.
2-en utilisant le theoreme du moment cinetique scalaire sur le systeme poulie ,ressort ,fil M1 et M2 , je dois determiner une relation entre x1'', x2'', m2, m1 et M.
j'ai fait J
'' = M(P1) + M(P2) + M(Ppoulie)
(les poids etant des vecteurs) , pour la poulie le moment est nulle,
ensuite on a x1'' = a'' et J= Ma2 et M(P1) = am1 et M(P2) = -am2
ainsi j'obtiens Mx1'' = g(m1-m2)
ce qui n'est pas tout a fait le resulat voulu.
Pouvez vous m'aider ?
merci
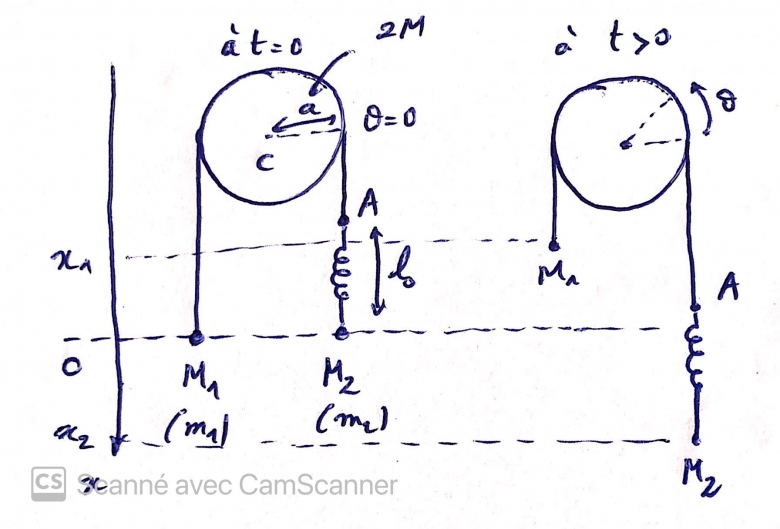
Bonsoir
j'ai du mal a ecrire AM2 en fonction de x1 et x2
Il faut considérer le fil entre A et MA inextensible et faire un schéma réaliste avec un maximum de grandeurs algébriques choisies positivement sur le schéma. Si tu choisis
>0 : selon ton schéma, la poulie à tourné dans le sens inverse de celui des aiguilles d'une montre ; puisque le fil ne glisse pas sur la gorge de la poulie, M1 est en dessous de sa position d'équilibre et on obtient :
x1=R.
;
Cette relation peut être dérivée deux fois par rapport au temps pour avoir une relation entre l'accélération angulaire de la poulie et l'accélération de M1.
D'autre part, le fil entre M1 et A est inextensible : quand M1 descend de la distance x1>0, le point A monte de la même distance :
xA=-x1
En appelant x2 l'abscisse de M2, facile alors d'obtenir l'allongement du ressort en fonction de x1 et de x2.
Enfin : le théorème du moment cinétique appliquée à la poulie fait intervenir les moments par rapport à l'axe de la poulie des moments des tensions exercée par le brin droit et le brin gauche du fil. Ces tensions ne sont pas égales aux poids des deux masses.
Je pense qu'un nouveau schéma où seraient représentés les différents vecteurs forces serait bien utile.
Petite rectification concernant le point A : comme déjà écrit : quand M1 descend de la distance x1>0, le point A monte de la même distance mais cela ne signifie pas xA=-x1 dans la mesure où les abscisses initiales de A et de M1 sont différentes. Cette remarque est utile pour déterminer en fonction de X1 et x2 l'allongement (L-Lo) du ressort.
Sinon : ce schéma pourra peut-être t'aider : à toi de bien le comprendre et d'y ajouter si nécessaire d'autres indications.
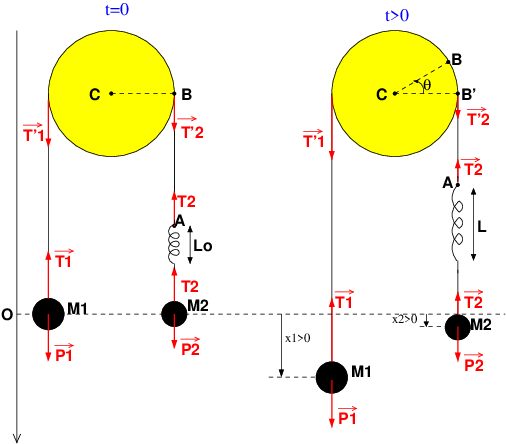
Bonjour
en m'aidant de votre schema, je trouve a partir de celui de gauche que xa + l0 = x1 (mais ce n'est pas forcement vrai pour t>0) **, ensuite avec celui de droite AM2 = x2 - xa et finalement
AM2 - l0 = x2 - x1
** puisque le fil est inextensible lorsque M1 se deplace de 
l = vt alors A se deplace de -vt , ainsi j'ecris x1(t) = x1(0) +vt = vt et xa(t) = xa(0) - vt = -l0 -vt
j'en deduis que xa + l0 = x1 est toujours valable.
Pour la deuxieme question. j'ai du mal a calculer certains moments.
en effet J '' = M(P1) + M(T2) + M(T'2) +M(T1) +M(T'1) + M(P1) ( devrais je mettre plutot 2M(T2) ? )
donc Max1'' = -am2g +ak(x2-x1) +M(T'2) + M(T1) +M(T'1) + am1g
en appliquant le PFD a M1 , je peux ainsi me débarrasser de M(T1)
j'obtiens ainsi Mx1'' = -m2x2'' +M(T'2) + M(T'1) +m1x1''
j'aimerais dire que les deux moments restants s'annulent entre eux , mais je ne vois pas trop comment le justifier
Rien ne permet d'affirmer que les mouvements de M1 et de M2 sont uniformes : les vitesses de ces deux masses ne sont pas a priori des constantes ; d'ailleurs, l'énoncé demande d'étudier les accélérations.
Les fils étant inextensibles, quand M1 descend de x1, le point A monte de x1 ; quand le point M2 descend de x2, l'extrémité inférieure du ressort descend aussi de x2. L'allongement du ressort est ainsi :
Relation fondamentale appliquée à M2 directement en projection sur l'axe des x :
Concernant le théorème du moment cinétique par rapport à l'axe de rotation passant par C et perpendiculaire au plan de figure, on calcule le moment du poids de la poulie comme si ce poids s'appliquait en C ; ce moment par rapport à l'axe est donc nul. Il faut donc uniquement tenir compte des moments des tensions des deux brins de fils :
J'imagine que les fils et le ressort sont supposés de masses négligeables : les normes des tensions se conservent donc le long de chaque brin de fil et le long du ressort ; en normes :
Remarque : pour éviter les erreurs de signes, j'ai représenté le système dans une position telle que les grandeurs x1, x2, soient positives. Cependant, les formules obtenues sont valides quels que soient les signes de ces grandeurs.
Annuler
connectez vous