Inscription / Connexion Nouveau Sujet
Potence supporter par un mur et par un tirant
Bonjour, je suis complètement perdu mais alors complètement et j'ai vraiment besoin de comprendre !
Donc est-il possible qu'on m'aide mais en m'expliquant (la réponse ne m'avancera rien sans explications) ?
Si vous êtes toujours motivé pour m'aider, voilà mon exo :
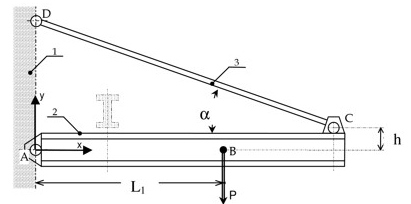
Une potence (2) est supportée par un mur (1) et par un tirant (3). Sur cette potence, en B, se situe un palan dont le poids est connu et noté P. Les points A, C et D sont des articulations, modélisées par des liaisons pivot. L'ensemble est supposé en équilibre. On néglige les poids de la potence (2) et du tirant (3). On pourra considérer qu'il s'agit d'un problème plan.
On note : L1=AB ; L=DC ; AC.y=h
On adoptera la syntaxe suivante pour l'écriture des torseurs de liaison :
Torseur de l'action de liaison en A d'un solide S0 sur un solide S1 : Ts(S0 S1)A =
S1)A =
{(R01Ax)(M01Ax)}
{(R01Ay)(M01Ay)}
{(R01Az)(M01Az)}
1) Donner la forme des torseurs de liaisons des efforts de (1) sur (3), de (1) sur (2) et de (2) sur (3). Vous exprimerez chacun de ces torseurs en son point de liaison et en prenant en compte l'hypothèse de problème plan. Combien d'inconnues de liaisons comporte ce problème ?
2) Exprimer le vecteur AD. dans le repère (A,x,y)en fonction de L, h, et  .
.
3) Appliquer, au point A, le principe fondamental de la statique à l'ensemble {(2) +(3)} (potence + tirant). En déduire un système de trois équations faisant intervenir les inconnues de liaison, le poids P et les dimensions du système.
4) Appliquer, au point D, le principe fondamental de la statique au tirant (3). En déduire un système de trois équations faisant intervenir les inconnues de liaison et les dimensions du système.
5) Déterminer les inconnues de liaison en fonction de P, L1, L, h, 
Pour la question 1) voilà se que j'ai "fais" :
Liaison pivot en D : {TS(S1 S3)}D =
S3)}D =
{(R01Dx) (0)}
{(R01Dy) (0)}
{(0) (0)}D
est-ce que je dois faire la liaison pivot en C de 1 3 ?
3 ?
Liaison pivot en A : {TS(S1 S2)}A =
S2)}A =
{(R01Ax) (0)}
{(R01Ay) (0)}
{(0) (0)}A
est-ce que je dois faire la liaison pivot de C de 1 2 ?
2 ?
Liaison pivot en C : {TS(S2 S2)}C =
S2)}C =
{(R01Cx) (0)}
{(R01Cy) (0)}
{(0) (0)}C
est-ce que je dois faire la liaison pivot de D et A de 2 3 ?
3 ?
Voilà est-ce que déjà je suis complètement à côté ou pas ?
Merci par avance de votre patience et de vos réponses
Cordialement
bonjour,
c'est ça, à part la notation: si j'ai bien lu, en D la réaction se note: R13Dx R13Dy
est-ce que je dois faire la liaison pivot en C de 1->3 ?
à ton avis, (1) et (3) n'étant pas en contact en C, peut-il y avoir une liaison?
Bonjour à tous,
avez-vous trouvé la réponse à cette question :
Combien d'inconnues de liaisons comporte ce problème ?
pour la 2)
je trouve : selon le vecteur unitaire y.
Je n'arrive pas à faire la question 3)
j'ai Ts(S1  S2)A + Ts(S1
S2)A + Ts(S1  S3)D = {0}
S3)D = {0}
donc mon système à 3 équations est :
R12Ax + R13Dx = 0 résultante en x
R12Ay + R13Dy = 0 résultante en y
et il me ma,que le moment en A comment puis-je le trouver ?
Merci pour votre aide
non c'est pas possible car à la fin je vais devoir retrouver mes valeurs L1, L, P, h et alpha et donc forcément dans le moment j'ai au moins du L, du L1 et du P
pour la question 1 où il faut que j'exprime chacun de ces torseurs en son point de liaison j'ai trouvé :
R12Dx = -P cos alpha
R12Dy = P sin alpha
est-ce correcte ?
bonsoir,
1) Liaison pivot en D : torseur {TS(S1->S3)}D =
{(R13Dx) (0)}
{(R13Dy) (0)}
{(0) (0)}
Liaison pivot en A : torseur {TS(S1->S2)}A =
{(R12Ax) (0)}
{(R12Ay) (0)}
{(0) (0)}
Liaison pivot en C : torseur {TS(S2->S3)}C =
{(R23Cx) (0)}
{(R23Cy) (0)}
{(0) (0)}
il y a en tout 6 inconnues de liaison
2) AD = (h + L sin  ) y (vecteurs en gras)
) y (vecteurs en gras)
3) on considère le système {(2)+(3)}
ce système est soumis aux torseurs de liaison {TS(S1->S3)} et {TS(S1->S2)}
et aussi au torseur correspondant à l'action du poids {T(P->S2)} dont les éléments de réduction en B sont : P et 0 (moment en B nul)
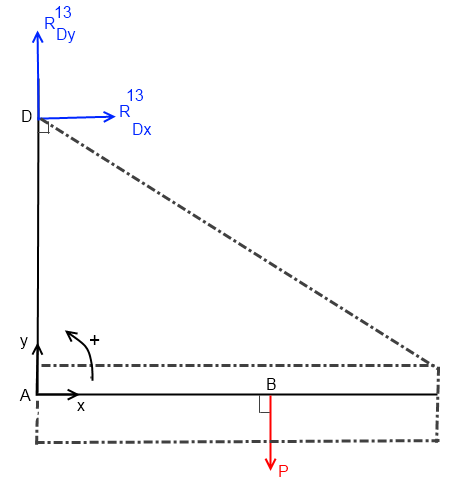
au point A, le principe fondamental de la statique s'écrit donc:
{TS(S1->S3)}A + {TS(S1->S2)}A + {T(P->S2) }A = 0T (torseur nul)
ce qui donne:
pour la résultante:
sur (Ax) R13Dx + R12Ax = 0
sur (Ay) R13Dy + R12Ay - P = 0
pour le moment en A: -PL1 - AD.R13Dx = 0
sauf erreur
entre temps je l'ai fais et j'ai comme toi donc j'ai compris, je suis contente 
par contre le moment en A je n'ai pas pareil mais comme je l'ai fait un peu au pif c normal. Peut tu me donner la formule pour calculer le moment en A ?
et me dire comme tu as fais ?
Merci
moment = force x bras de levier
donc ici c'est très simple puisque les seules composantes qui interviennent en A sont R13 Dx et P
et elles sont normales à la droite d'action (cf dessin)
toutes les autres ont un moment nul par rapport à A
pour ce qui est du signe, R13 Dx et P tendent à faire tourner dans le sens rétrograde donc signe -
NB je n'ai pas représenté la réaction en A puisque son moment en A est forcément nul
sauf erreur
Pour le moment en A j'ai trouver L1.R13Dy + hP en me servant d'autre exercice du même genre mais dans tout les cas, je pense que h doit apparaître, non ?
même avec le document je ne comprend pas comment trouver la formule !
Sur ton dessin tu as mis une flèche avec un +, ça signifie que la rotation se fait comme ça ?
Par contre pourquoi tu utilise R13Dx et non R13Dy ? ça je ne comprend pas
Sur ton dessin tu as mis une flèche avec un +, ça signifie que la rotation se fait comme ça ?
la flèche indique l'orientation du plan (Axy), on tourne dans le sens positif si on amène (Ax) sur (Ay)
imagine qu'en A il y ait un écrou et que AD soit une clé à molette
à ton avis: si tu tires en D selon RDy, est-ce que ça va faire tourner l'écrou ?
idem selon RDx ?
2ème question: dans quel sens va tourner l'écrou?
Je pense avoir compris donc j'ai fais la question 4)
Ts (S1  S3)D + Ts(S2
S3)D + Ts(S2  S3)C = 0
S3)C = 0
R13Dx + R23Cx = 0
R13Dy + R23Cy = 0
moment en D :
AD.R13Dx - AC.R23Cy = 0
est-ce correcte ?
oui, donc tu vois bien que le moment de RDy est nul en A (puisque cette force ne tend pas à faire tourner l'écrou en A )
tandis que RDx, elle, exerce bien un moment en A, et dans le sens négatif (d'après l'orientation du plan (Axy)
ensuite pour le bras de levier, je te renvoie au document.
ici P est orthogonale à AB donc son moment par rapport à A vaut (en module) P.AB (AB est le bras de levier)
RDx est orthogonale à AD donc son moment par rapport à A vaut: RDx . AD (AD est le bras de levier)
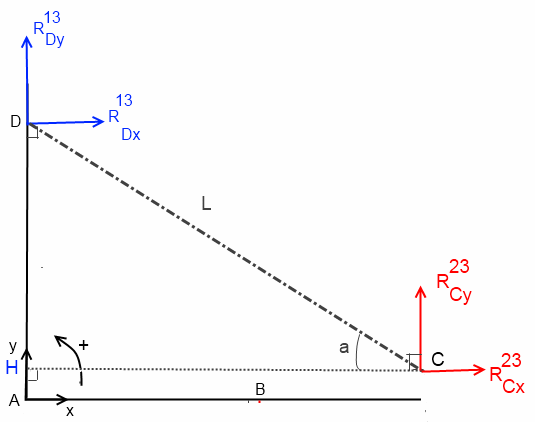
4) Appliquer, au point D, le principe fondamental de la statique au tirant (3).
résultante: ok
moment en D: (cf dessin)
Rcx.HD + Rcy.HC = 0
avec HC = L cos
et HD = L sin
la force RDx a un moment nul par rapport à D puisqu'elle s'applique en D
imagine qu'en D il y ait un écrou: si tu tires selon RDx directement sur l'écrou, ça m'étonnerait qu'il tourne
imagine que DH soit une clé à molette
si tu tires en H selon Rcx dans quel sens tourne l'écrou?
imagine que DC soit une clé à molette
si tu tires en C selon Rcy, dans quel sens tourne l'écrou?
Je ne sais pas si tu l'es mais faut que tu fasses prof ! J'ai tout compris et le coup de l'écrou et de la clé ça passe trop bien ^^ merci je vais pouvoir faire mes deux autres exercices.
Juste une dernière question, si on tourne dans le sens des aiguilles d'une montre on met un - c'est ça ?
Merci beaucoup
Juste une dernière question, si on tourne dans le sens des aiguilles d'une montre on met un - c'est ça ?
ça dépend de l'orientation du plan.
ici le sens positif est le sens trigo (cf mon dessin), donc effectivement on met un - si on tourne dans le sens des aiguilles d'une montre
en général c'est cette orientation qui est utilisée.
mais ce n'est pas une obligation, on peut orienter un plan dans le sens inverse (en inversant ici Ax et Ay par ex.)
(c'est pour cela qu'il vaut mieux mettre une flèche + pour bien montrer l'orientation)
Cher Grignotin, il faut finir les exercices pour demain, bonne chance
il me manque le deuxième exercice pour ma part


