Inscription / Connexion Nouveau Sujet
position équilibre deux ressorts un pendule
Bonsoir,
je me demandais si il était possible de trouver la position d'équilibre du système que je vais décrire en dessous, sans passer par les énergies? par exemple par le pfd?
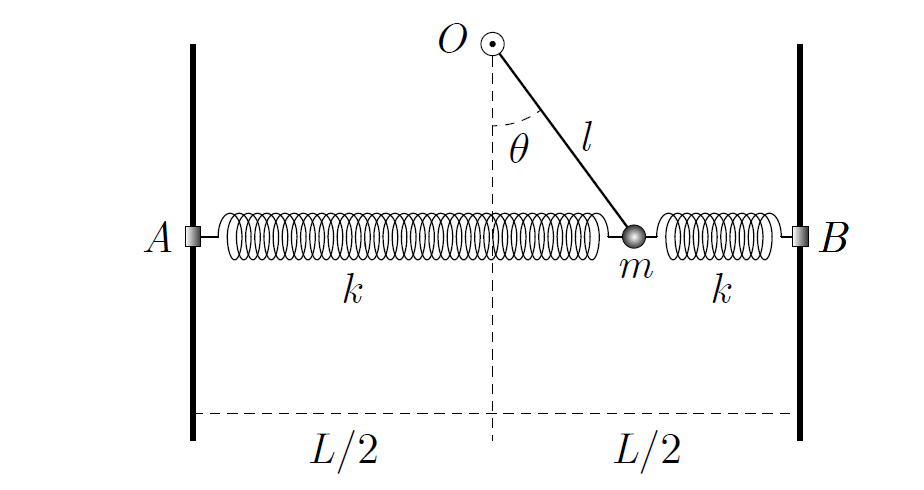
il s'agit d'un point M de masse compris dans une boite, accroché au plafond au milieu et de chaque coté un ressort de longueur à vide la largeur de la boite sur 2.
La longueur du pendule est R, et les ressorts sont accroché à R du plafond.
Les deux ressorts ont des constantes k différentes.
Qu'en pensez vous?
merci et bonne soirée!
pardon les deux ressorts ne sont pas accrochés à R du plafond mais peuvent bouger 
ainsi ils pourraient se retrouver au dessus du pendule.
Merci!
Bonjour
La description du dispositif que tu fournie n'est pas vraiment claire... Pourrais-tu joindre un scan d'un schéma de ce dispositif ?
Magnifique ce schéma ! Si tu l'as fait toi-même, tu es vraiment un pro sous TeX !
Petite remarque tout de même : c'est un très bon schéma de "principe" mais en pratique, il faudrait imaginer une tige rigide horizontale de masse négligeable devant m, reliant A à B sur lequel les deux ressorts seraient enfilés. La boule de masse m devrait aussi être enfilée sur cette tige, un peu à la manière d'une perle. Sinon, impossible de maintenir sur une même horizontale les axes des deux ressorts et le centre d'inertie du solide de masse m.
La position d'équilibre stable est bien sûr la position 
=0. Cela se prouve en montrant que cette position correspond à un minimum d'énergie potentielle.
On peut aussi appliquer au solide de masse m le principe fondamental de la statique :
puisque les deux ressorts sont identiques, les deux forces qu'ils exercent sur le solide de masse m se compensent si =0. Le poids du solide est dans ce cas compensé par la tension du fil de longueur l.
C'est l'étude des oscillations et de leur période qui est physiquement intéressante !
merci pour les compliments.
On peut alors trouver la position 0 mais il y en a bien d'autres, autant stables qu'instables. Notamment pi dans certains cas (gros coefficient de ressorts) mais aussi encore d'autres positions. Ainsi, est-il possible de les trouver par le PFD par exemple?
merci
Tu supposes les deux ressorts de raideurs différentes : k et k' par exemple ; que valent leurs longueurs à vide ? Tu supposes, je pense, la liaison entre la masse m et l'axe passant par O rigide (tige et non simple fil). Tu envisages aussi les cas où (AB) est au-dessus du point O.
Franchement, dans cette situation : l'outil le plus adéquat est l'énergie potentielle : à un maximum local de Ep correspond un équilibre instable, à un minimum local de Ep correspond un équilibre stable. Il suffit d'étudier la courbe Ep=f() pour s'en sortir. La relation fondamentale de la statique appliquée à la masse m est une méthode possible mais beaucoup plus compliquée à mettre en oeuvre. De plus cette méthode, contrairement à la précédente, ne permet pas simplement de déterminer le caractère stable ou instable de l'équilibre.
Annuler
connectez vous