Inscription / Connexion Nouveau Sujet
Portrait de phase d'un oscillateur à deux ressorts.
Bonjour je connais quelques problemes sur cette exercice pouvez-vous m'aidez svp !
On considère le système présenté figure 1.a, constitué de 2 ressorts identiques de caractéristiques (k,lo), dans un plan horizontale. Le point M, de masse m, est mobile sans frottement sur une tige, il se déplace uniquement sur l'axe (Ox). Il est initialement à sa position d'équilibre et lâché avec une vitesse initiale Vo.(Désolé pour les figures je ne les est pas scanné, mais vu ce qui est décrit dans le texte, j'espere que vous trouverez comment son les schémas).
1. Justifier avec soin l'intérêt de l'approche énergétique. Montrer que l'énergie potentielle du point est Ep = kx² - 2k
(a²+x²) + 2kloa, si on impose Eptot (x=0) = 0. Exprimer Ep/ka² en fonction de u = x/a. Bon sur cette partie sava, j'ai bien trouver cette énergie potentielle et en remplacant avec u, je trouve u²-2lo((1+u²)/a)-2lo/a.
2. Repérer les positions d'équilibres et discuter leur stabilité graphiquement. Commenter. Ici si d²Ep/dt²
0 alors équilibre stable sinon si d²Ep/dt²
0 alors équilibre instable.
3. Trouver l'équation différentielle du mouvement x(t). On pose 
²= 2k/m, To = 2
/o , et 
= t/To. Montrer que l'équation différentielle de u = x/a est d²u/d² + 4²u(1-
/(1+u²)) = 0. Bon ici je seche, faut-il appliquer le pfd, si oui faut-il projeter et qu'est-ce que sa devient ? Faut t'il dérivée l'équation énergétique pour retouver l'équation différentielle ? Pouvez vous m'aidez svp !
Bonjour.
Si on te demande de calculer l'énergie potentielle, ce n'est pas pour revenir au PFD par la suite. Il faut dériver l'expression de l'énergie mécanique (constante puisque pas de force non conservative) pour avoir l'équa diff du mouvement.
Cela dit, l'énoncé est un peu juste pour se figurer exactement la configuration du système...
@+
Oui et croit bien que j'en suis désolé, d'accord pour la dérivée de Ep mais qu'est-ce que sa va donner alors.........
dEp/dt = 2kx - (2klo*2x*2a)/2(a²+x²) + 0. Est-ce bon ?
Salut.
Avant de te répondre, je voudrais savoir comment sont disposés les ressorts par rapport à la tige, et ce qu'est a.
@+
Alors tu a tes axes x et z et a represente la longueur entre le point O d'origine jusqu'a la hauteur du ressort sur l'axe z (je sait, c'est pas tres clair......) et x represente la longueur sur l'axe des x entre l'origine et l'éttirement du ressort en gros, un ressort forme avec les 2 axes un triangle rectangle, et comme il y a 2 ressorts identiques, cela forment 2 triangles symétrique par rapport a l'axe des x.
Re.
Donc, deux ressorts identiques alignés au repos suivant Oz dont on étudie les vibrations transversales ...
On t'a fait calculer l'énergie potentielle normalisée Ep/ka2 en fonction de l'élongation normalisée u = x/a.
De même, on peut exprimer l'énergie cinétique normalisée Ec/ka2 en fonction de du/dτ en faisant les changements de variables demandés.
L'objectif de cette normalisation est d'alléger un peu les expressions. Cela ne change rien sur les principes à appliquer.
Puisqu'il n'y a que des forces conservative, l'énergie mécanique Em = Ep + Ec = Cte, donc l'énergie mécanique normalisée Em/ka2 = Ep/ka2 + Ec/ka2 = Cte. Donc la dérivée de l'énergie mécanique normalisée par rapport à τ est nulle. C'est comme cela qu'on obtient l'équation différentielle du mouvement par les méthodes énergétiques.
On arrive classiquement à une expression du genre du/dτ ( ) = 0, et c'est le machin entre parenthèses qui nous intéresse. Il suffit d'y faire les changements de variables demandés pour arriver à l'expression donnée.
Cela se fait sans difficulté. Faut pas se planter dans les changements de variables, c'est tout.
@+
Elle est fausse ! Tu as manifestement un problème avec la dérivation des fonctions composées.
Je te suggère de revoir d'urgence ce point de cours avant de poursuivre.
C'est un truc à se planter royalement pendant les contrôles/examens/concours, et ce serait vraiment trop c..
@+
j'avoue, attend je la refait e je te reposte sa ! C'est avec le terme (a²+x²) que g du mal pcq avec les constante c chiant ^^
Donc le terme avec la racine devient 0 le terme d'apres aussi il reste donc kx² a dérivée et c tout, ce qui donne 2kx'x.
Aïe, aïe, aïe.
Rappel de math de terminale :
La dérivée de a f(u) (a constante) par rapport à u est a f'(u).
Si u = u(x), alors la dérivée de a f(u) par rapport à x est a f'(u) u'(x).
Ici :
d(2k(a²+x²)1/2)/dt = 2k d((a²+x²)1/2)/dt (on sort les constantes multiplicatives)
d((a²+x²)1/2)/dt = 1/2 (a²+x²)-1/2 d(a²+x²)/dt = 1/2 (a²+x²)-1/2 2 x x' (la dérivée de a²+x² par rapport à t est 2 x x')
Donc d(2k(a²+x²)1/2)/dt = 2 k (a²+x²)-1/2 x x' après simplification
Bon, je n'ai pas envie de rester planté là à attendre une réponse.
Je suis disposé à consacrer du temps aux autres, mais je n'aime pas le perdre.
Je trouve regrettable de rester en rade pour des calculs de dérivées élémentaires qui conduisent à laisser la physique de côté.
Deux choses à voir dans ce problème :
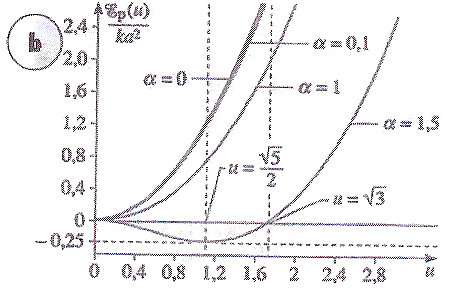
1 - l'étude de stabilité est à mener en fonction du rapport lo/a. On s'aperçoit, en effet, que si a < lo, la position x=0 est une position d'équilibre instable. Les positions d'équilibre stables sont alors symétriques de par et d'autre de l'axe de symétrie. Si a >= lo, on a alors plus qu'une seule position stable pour x=0.
2 - autour d'une position d'équilibre stable, il est possible de linéariser l'équation différentielle du mouvement pour les petits déplacements. On a alors affaire a un oscillateur harmonique.
Excuse moi, je n'était pas la ! D'accord merci pour les rapelles de dérivées... !!!!!! Donc l'équation du mouvement de x(t), il faut dérivée l'équation énergétique soit Em = Ep + Ec. Ep est donc kx² + 2klo(a²+x²) + 2kloa. et Ec = 1/2mV² comme il part avec une vitesse initiale Vo, donc Ec(t=0)=1/2mVo², donc Em(t)=Ep(t)+Ec(t) soit Em(t=0)=1/2mVo² + kx² + 2klo(a²+x²) + 2klo*a = 0. Et il faut dérivée sa pour avoir le mouvement de x(t), c'est sa !!
Bonjour.
Attention, quand il n'y a que des forces conservatives comme ici, c'est l'énergie mécanique (Ep+Ec) qui est constante alors que Ec et Ep varient au gré du déplacement du point M. Ec a une valeur initiale à t = 0, mais Ec(t) n'est pas tout le temps égal à Ec(0).
Donc, ce que tu as écrit n'est pas correct.
Voila deux images qui t'aideront pour la question 2, pour l'étude des points d'équilibres, l'étude dans ce probleme ce concentre sur les courbes =0 et =1.5..
Annuler
connectez vous