Inscription / Connexion Nouveau Sujet
Portrait de phase
Bonjour à tous et bonne fête de fin d'année. Svp j'ai besoin d'aide.
L'énergie potentielle d'un système est donnée par U(x)=.
Representer le plan de phase (je n'ai pas eu de problème pour esquisser). Je n'arrive par contre pas à repérer les mouvements oscillatoires harmoniques et anharmoniques sur le plan de phase. La photo représente le tracé de l'énergie potentielle en fonction de x.
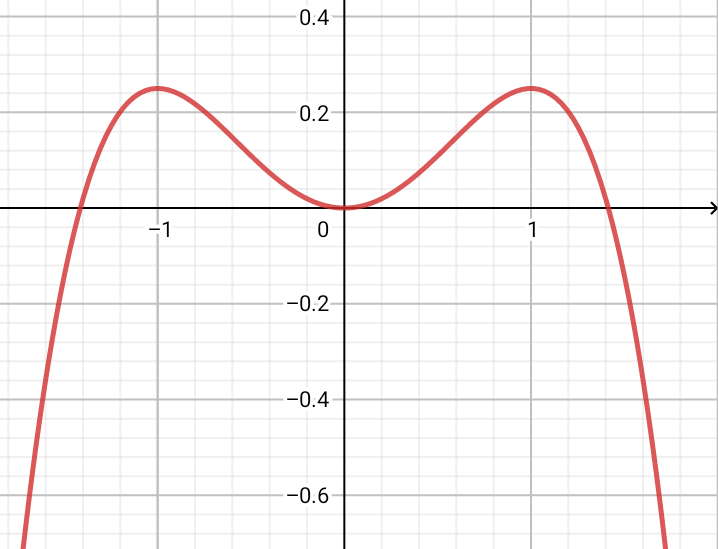
Bonjour
Tu peux déjà essayer de comprendre qualitativement les diverses situations à partir de la courbe Ep=f(x) que tu viens de tracer.
Si l'énergie mécanique est inférieure à Epmax, la particule va osciller dans la cuvette de potentiel. Si |x| n'est pas trop grand, on pourra poser :
Ep
k.x2/2
Le fond de la cuvette de potentiel est analogue à une parabole : le mouvement est harmonique. Écris l'équation différentielle vérifiée par x pour t'en convaincre.
Si Em>Ep : pas d'oscillation ; mouvement anharmonique
Si Em<Epmax, je pense qu'en plus d'un mouvement oscillatoire on peut avoir des mouvements infinis à gauche et à droite. Proche de la position d'équilibre (x=0), le système peut se réduire à un oscillateur harmonique qui se démontre en faisant un DL autour de x=0. Pour Em>Epmax, on a un mouvement infini qui commence à - l'infini et va à + l'infini. Je ne comprends pas pourquoi il s'agit là d'un mouvement anharmonique. J'ai lu quelque part qu'une l'oscillation est dit anharmonique si le système évolue suivant une loi périodique de forme quelconque non sinusoïdale. Je ne vois pas en quoi cette définition est respectée dans ce cas.
J'aimerais aussi savoir quelle est la différence entre mouvement oscillatoire linéaire et mouvement oscillatoire non linéaire. Comment les identifier ?
Il y a oscillations harmoniques lorsque le mouvement est sinusoïdal, l'équation horaire étant de la forme :
x=Xm.cos(
.t+
) avec :
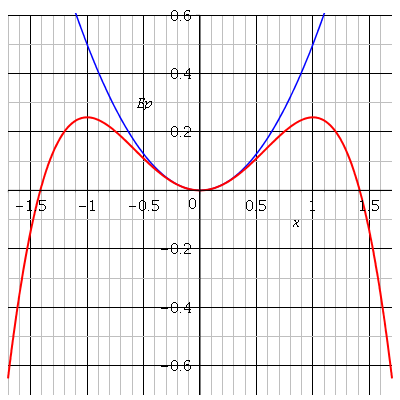
Dans ce cas l'énergie potentielle est Ep=k.x2/2. On voit bien graphiquement que cela se limite au cas où la cuvette de potentiel se confond avec la parabole d'équation Ep=k.x2/2 (courbe bleue). Tout dépend de la précision demandée mais, on voit bien qu'approximativement, cela correspond à Xm<0.35 environ soit Em<0,07k environ.
Pour 0,07k<Em<Epmax on obtient un mouvement oscillatoire anaharmonique. l'équation différentielle vérifiée par x est : . Le mouvement est oscillatoire périodique mais non sinusoïdal.
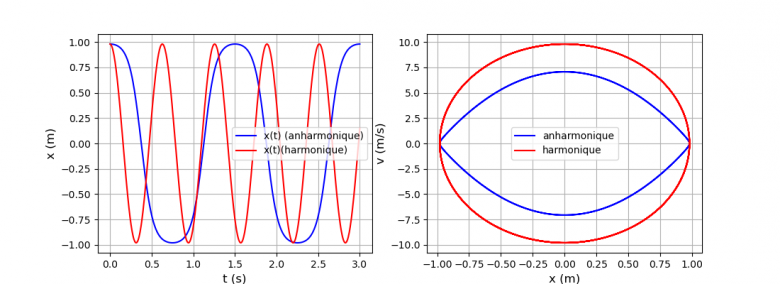
Ces courbes que je te laisse interpréter.
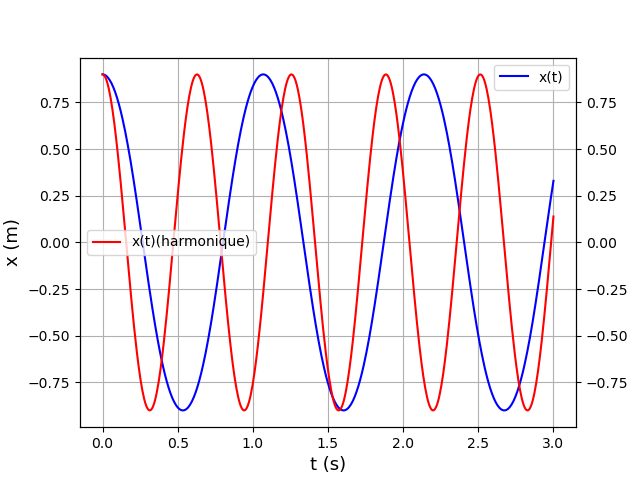
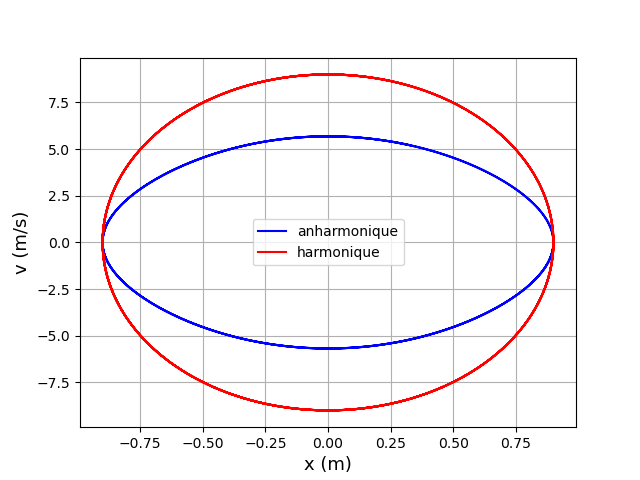
En rouge : la courbe x=f(t) et le portrait de phase pour une amplitude Xm=0,9m : bien sûr les oscillations ne sont pas sinusoïdales. Noter la forte augmentation de la période due à la force en kx3.
En bleu : la courbe théorique et le portrait de phase pour une même valeur du rapport k/m, une même amplitude Xm mais une simple force de rappel en seulement (-kx). Les oscillations sont sinusoïdales.
Merci beaucoup. Je ne savais pas qu'une force en kx3 fait augmenter la période. (peux-tu stp mieux expliquer ?) Le graphe de x=f(t) s'est résolu numériquement (ie on est quitté de l'équation différentielle du mouvement)?
Je constate que sur le portait de phase, la vitesse maximale (vitesse à l'équilibre) et toutes les autres vitesses sont réduites par rapport à celles pour un oscillateur harmonique. Ceci se justifie par le fait que dans ce cas la période a augmenté. Puisque l'amplitude est restée inchangée, la vitesse doit nécessairement diminuer.
Remarque préliminaire que j'aurais sans doute dû faire dès le début : tu es j'espère habitué à raisonner littéralement et à vérifier l'homogénéité des formules obtenues. Que penser de l'homogénéité de la formule proposée par l'énoncé :
et de celle qui en découle sur la résultante des forces :
???
J'en reviens à ta question :
Je ne savais pas qu'une force en kx3 fait augmenter la période
C'est plutôt que, lorsqu'on se rapproche des "bords" de la cuvette, la résultante des forces
1 sont des positions d'équilibre (certes instables. Supposons qu'il soit possible d'abandonner la particule en x=1 sans vitesse initiale : la particule resterait immobile.
Pour illustrer cela voici le portrait de phase pour Xm=0,98. La période est encore plus grande. La courbe x=f(t) (en bleu) est plus "arrondie" à ses extremum, signe d'une vitesse plus faible pour |x| grand mais cela ne signifie pas une vitesse plus faible (au contraire !) aux passages en x=0.
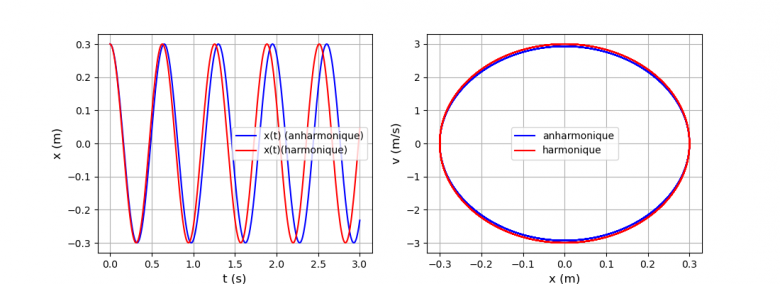
Je te fournis aussi le diagramme pour Xm=0,3 : il est quasiment confondu avec celui de l'oscillateur harmonique comme prévu précédemment.
Ah d'accord. La force en kx3 suppose que le coefficient 1 devant kx3 a une dimension telle que kx3ait la dimension d'une force. On peut retrouver la dimension de 1 par une application directe de l'analyse dimensionnelle.
(Stp avec quoi fais-tu les schémas que tu postes ?)
kx3 ait la dimension d'une force
Pas tout à fait. Remarque fondamentale : on ne peut en physique additionner ou soustraire que des grandeurs de même dimension. Additionner un volume à une longueur n'as pas de sens. C'est pourtant ce que propose l'énoncé !
Je prends la formule directement déduite de l'expression fournie de l'énergie potentielle :
avec "a" ayant la dimension d'une longueur. Rien n'empêche bien sûr de poser pour les applications numériques a= 1m.
Cela conduit à une expression homogène de l'énergie potentielle :
Ainsi, dans le cas général, l'oscillateur est équivalent à un oscillateur harmonique pour |x| petit devant "a".
Stp avec quoi fais-tu les schémas que tu postes ?
Pour les représentations graphiques et la résolution numérique de l'équation différentielle :
J'explique paragraphe IV de ce document comment résoudre numériquement une équation différentielle par la méthode d'Euler. Le reste du document est largement hors sujet même s'il s'agit de mécanique.
Pas tout à fait. Remarque fondamentale : on ne peut en physique additionner ou soustraire que des grandeurs de même dimension. Additionner un volume à une longueur n'as pas de sens. C'est pourtant ce que propose l'énoncé !
Je prends la formule directement déduite de l'expression fournie de l'énergie potentielle :
avec "a" ayant la dimension d'une longueur. Rien n'empêche bien sûr de poser pour les applications numériques a= 1m.
Cela conduit à une expression homogène de l'énergie potentielle :
Ainsi, dans le cas général, l'oscillateur est équivalent à un oscillateur harmonique pour |x| petit devant "a".
Je me suis peut-être mal exprimé mais je disais la même chose. Le 1 dont je parlais est ce "a" que tu as posé.
j'utilise par habitude un programme sous Python mais cela peut aussi se faire assez facilement avec un simple tableur type LibreOffice ou Excel.
Merci beaucoup. Sans avoir l'intention d'en faire trop, j'aimerais aussi savoir le logiciel ou l'application qui te permet qui de faire des dessins quelconques (modélisation d'un problème, d'une situation physique, d'un circuit électrique...) ou d'autres applications de ce type à accès au grand public.
J'utilise comme système d'exploitation de mon pc : linux plutôt que windows (linux : totalement gratuit, sans pub et mieux sécurisé). Pour les dessins simples, en particulier pour les circuits électriques, j'utilise DIA : bonne qualité à l'exportation et à l'impression et facilité d'utilisation. Je sais qu'il en existe une version pour windows téléchargeable gratuitement. Pour les schémas plus complexes (en mécanique en particulier), j'utilise XFIG : un peu plus délicat à utiliser et à installer sous windows.
J'aimerais aussi savoir quelle est la différence entre mouvement oscillatoire linéaire et mouvement oscillatoire non linéaire. Comment les identifier sur un graphe de l'Ep ou du portait de phase?
Stp j'ai encore cette question.
On parle plutôt d'équation différentielle linéaire ou non.
x=f(t) est solution d'une équation différentielle linéaire d'ordre n si on peut écrire :
(K : constante)
On rencontre essentiellement en physique des équations différentielles d'ordre 1 (décharge d'un condensateur à travers une résistance, décroissance radioactive, cinétique chimique d'ordre 1...) et des équations différentielles d'ordre 2 (beaucoup en mécanique, décharge d'un condensateur à travers une bobine...). Si la résolution de ce type d'équation te pose problème, tu peux éventuellement consulter cette fiche :
Ici : l'équation différentielle est linéaire d'ordre 2 et admet une solution sinusoïdale (oscillateur harmonique).
L'équation différentielle : n'est pas linéaire et n'admet pas de solution sinusoïdale. Il faut la résoudre numériquement : la solution est impossible à exprimer à l'aide de fonctions mathématiques simples.
Si l'équation différentielle admet une solution sinusoïdale, la courbe Ep=f(x) est une parabole : ; sinon : la courbe Ep=f(x) n'est pas une parabole (voir courbes du 31-12-23 à 14:03).
Si l'équation différentielle admet une solution sinusoïdale, le diagramme des phases est une ellipse ou un cercle (voir courbes du 02-01-24 à 04:23)
Annuler
connectez vous