Inscription / Connexion Nouveau Sujet
Portée mer-mer
Bonjour, j'aimerais un peu d'aide pour cet exercice. Merci
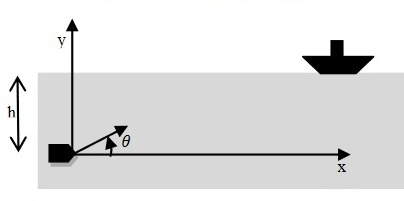
Un missile de masse, de volume V, est tiré d'un sous-marin en plongée à une profondeur h, avec une vitesse faisant un angle
 avec l'horizontale. La masse volumique de l'eau est notée
avec l'horizontale. La masse volumique de l'eau est notée  . On néglige le frottement de l'air. Le frottement dans l'eau esrt modélisée par
. On néglige le frottement de l'air. Le frottement dans l'eau esrt modélisée par où c est une constante positive Déterminer la portée R du missile en admettant que celui ci est pesé c'est à dire que m =
 V et en supposant que le missile a une phase hors de l'eau.
V et en supposant que le missile a une phase hors de l'eau.
Bonjour, j'aimerais un peu d'aide pour cet exercice. Merci
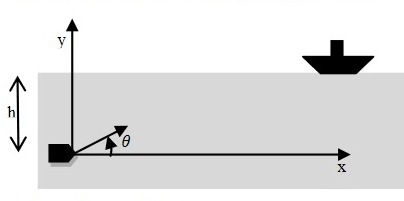
Un missile de masse, de volume V, est tiré d'un sous-marin en plongée à une profondeur h, avec une vitesse faisant un angle
 avec l'horizontale. La masse volumique de l'eau est notée
avec l'horizontale. La masse volumique de l'eau est notée  . On néglige le frottement de l'air. Le frottement dans l'eau esrt modélisée par
. On néglige le frottement de l'air. Le frottement dans l'eau esrt modélisée par où c est une constante positive Déterminer la portée R du missile en admettant que celui ci est pesé c'est à dire que m =
 V et en supposant que le missile a une phase hors de l'eau.
V et en supposant que le missile a une phase hors de l'eau.
[img1]
*** message déplacé ***
Lorsque je fais les équations paramétriques, je détermine l'equation cartésienne, je trouve la portée comme vu en terminale.
Mais je me dit que c'est pas ça car je n'ai pas eu à utiliser les forces de frottements ni la masse
*** message déplacé ***
Bonjour pfff
peux-tu modifier ton profil s'il te plaît, il me semble que tu n'es plus en terminale...

Bonjour à vous deux,
Et tu ne peux pas passer de terminale à math spé : cela correspond à la deuxième année de classe préparatoire aux grandes écoles !

Bonjour
Tu as deux études successives à faire : l'étude du mouvement dans l'eau puis l'étude du mouvement dans l'air.
L'étude du mouvement dans l'air est faite dès l'enseignement secondaire.Pour l'étude du mouvement dans l'eau, la méthode est analogue. Il faut partir de l'inventaire des forces, de l'expression de la relation fondamentale de la dynamique puis de la résolution de celle-ci. N'oublie pas le théorème d'Archimède. Dans le cas particulier m = V, la nature de mouvement est particulièrement simple...
V, la nature de mouvement est particulièrement simple...
Je te laisse réfléchir et proposer une solution...
Bonjour pfff
peux-tu modifier ton profil s'il te plaît, il me semble que tu n'es plus en terminale...

D'accord
Bonjour à vous deux,
Et tu ne peux pas passer de terminale à math spé : cela correspond à la deuxième année de classe préparatoire aux grandes écoles !

Oui oui ca fait deux ans que je n'ai pas modifié le profil. J'etais en prépa MPSI l'année passée
pour l'étude du mouvement dans l'air :
Voici l'equation du mouvement que je trouve
mais il n'y a pas les valeurs numériques pour resoudre y =0 donc je ne vois pas comment trouver.
Dans l'eau :
d'après le théorème du centre d'inertie on a :
c'est trop te demander de modifier ton profil ? combien de demandes va-t-il falloir faire ? 
ton sujet est verrouillé tant que cela n'est pas fait
tu feras un signalement en bas de page pour qu'on le déverrouille une fois ton profil modifié
Veuillez m'excuser, je croyais l'avoir fait, je n'ai pas appuyé sur modifier
*** message déplacé ***
ah ben dis donc il a quand même fallu employer les grands moyens ...
*** message déplacé ***sujet déverrouillé  ***
***
OK pour l'équation de la trajectoire dans l'air.Tu devrais pouvoir en déduire l'expression de la portée dans l'eau, c'est à dire la distance entre le point de sortie de l'eau et le point où le missile retombe dans l'eau ou sur le bateau.
Pour le mouvement dans l'eau : tu sembles oublier le poids. De plus, si m= .V , que peux-t-on dire de la somme vectorielle de ces deux forces ? La relation fondamentale de la dynamique prend alors une forme très simple et la trajectoire est ainsi particulièrement simple... Très facile alors d'obtenir l'abscisse du point de sortie de l'eau.
.V , que peux-t-on dire de la somme vectorielle de ces deux forces ? La relation fondamentale de la dynamique prend alors une forme très simple et la trajectoire est ainsi particulièrement simple... Très facile alors d'obtenir l'abscisse du point de sortie de l'eau.
leur somme vectorielle est égale au vecteur nulle ?
mais ça revient au fait que P = donc l'équation que j'ai trouvé ne change pas
et puis pour l'équation de la trajectoire dans l'air, ce n'est pas possible de trouver l'expression avec le h qui ne facilite pas la tache
mais sinon j'ai trouvé une autre manière de trouver l'expression :
on a :
x =
donc y = 0 donne
le discrimiant est :
donc on trouve deux solutions :
j'ai pris la solution la plus certaine positive donc t =
en remplaçant t dans x j'obtiens la portée qui est
Il faut commencer par étudier le mouvement dans l'eau.Le schéma te fournit la réponse concernant la nature de la trajectoire : à toi de faire une démonstration rigoureuse. Il te faudra ensuite trouver la valeur de la vitesse V'o du missile sortant de l'eau. Ce n'est qu'ensuite que tu pourras étudier la trajectoire dans l'air ; je te conseille de le faire dans le repère (O',x',y'). Ton calcul de portée est compliqué et erroné ; il est plus simple de déduire la portée dans l'air de l'équation de la trajectoire parabolique dans l'air.
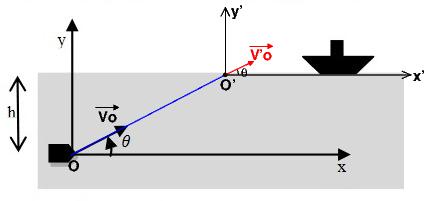
le missile quitte l'eau quand y(t) = h.
Donc : xO' = ? Ce résultat est utile pour trouver la portée totale : distance parcourue horizontalement dans l'eau plus distance horizontale parcourue dans l'air avant de retomber à l'eau ou sur le bateau.
La trajectoire dans l'eau est rectiligne
Tu ne fais aucune démonstration ! Relis mon message du 22-08-21 à 18:04 ; de plus, il est nécessaire de déterminer les caractéristiques du vecteur
Bonjour, excusez pour la longue attente.
Tu ne fais aucune démonstration !
Excusez moi
Dans l'eau
finalement
Le mouvement est donc rectiligne uniforme
La portée dans l'air fait intervenir la vitesse de sortie de l'eau VO' qui est inférieure à la vitesse de lancement Vo.
Malgré tout tes efforts pour l'éviter, il est indispensable de faire une étude détaillée du mouvement dans l'eau pour obtenir cette vitesse de sortie de l'eau. Je t'ai déjà expliqué la méthode de façon détaillée...
Franchement : tu postes au niveau math spé et tu ne réussis pas à écrire correctement la relation fondamentale de la dynamique ???
Écrire :
suppose un vecteur vitesse ayant la direction du vecteur