Inscription / Connexion Nouveau Sujet
Portait de phase : analyse qualitative
Bonjour.
Encore une fois je fais appel à vous et sollicite un peu d'aide pour un exercice qui me fait un peu perdre la tête...
Je joins dans mon prochain message le portait de phase en question - pourvu que ça marche...
Voici la situation :
Un anneau assimilé à un point M se déplace le long un cerceau vertical de centre O. On note A la position la plus basse.
Le mouvement de M est décrit par l'angle  entre OA et OM.
entre OA et OM.
Conditions initiales : à t=0 M est à la position la plus basse et on lui communique une vitesse v0.
1) Expliquer comment le point peut se déplacer selon la valeur de v0 et justifier l'existence d'une vitesse v0(lim).
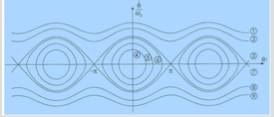
2) Faire l'analyse du portait : pour chaque courbe, donner la valeur de v0, identifier le point de départ et le sens de parcours.
3) Pourquoi 3 et 7 ont des points communs ?
Cet exercice me perturbe car je ne comprends pas ce qu'il se passe.
Et en plus, comment trouver v0?
J'ai noté cependant que : plus v0 est grande, plus le système oscille longtemps et sa trajectoire est a priori une ellipse pour commencer. Mais comment expliquer les trajectoires 1 et 2 par exemple ?
Merci beaucoup pour votre aide.
Si vous ne voyez pas bien les numéros, je mets leurs positions :
- au milieu on a 4 puis 5 puis 6
- à droite, de haut en bas, 1,2,3,7,8,9
Hello
La résolution de l'image, plus que celle du problème, en est un 
Je pense que le "portrait de phase" est dans ton cours. Juste pour le cas où, dans le plan de phase (abscisses: , ordonnées
) on va dessiner les trajectoires possibles selon les différentes conditions initiales (caractéristiques)
en supposant qu'il n'y a pas de frottements ..., tu peux par exemple écrire que l'énergie mécanique se conserve, en prenant comme origine de l'énergie potentielle (de pesanteur  ) le point A.
) le point A.
Tu exprimes tout cela en fonction de et
Et tu calcules la constante en fonction des conditions initiales
Tu dois arriver à quelque chose comme (aux "toujourspossiblesétourderiesdemapart" près)
Qui peut également s'écrire (si si là c'est un "indice")
Et là tu dois commencer à pouvoir fixer les conditions pour que la vitesse angulaire s'annule ou pas ...
A toi ...