Inscription / Connexion Nouveau Sujet
Point elastiquement lié a un support circulaire
Voici l'énoncé :
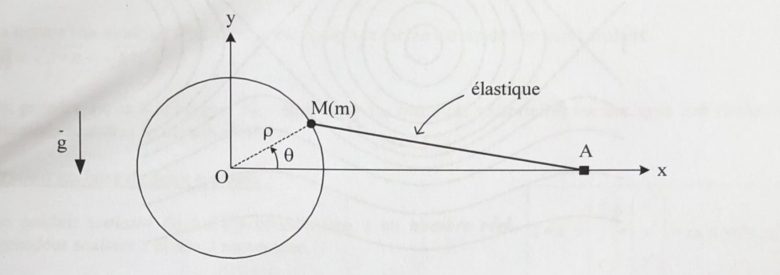
Une perle M, de masse m, est enfilée sur un support circulaire fixe, de centre O et de rayon r, contenu dans le plan vertical (Oxy). La position de M sur le cerveau est repéré par l'angle θ. De plus, la perle est attaché à un elastique de raideur k, dont l'autre extrémité est fixée en A. L0 <<L donc on néglige L0 devant la distance L=AM.
La position du point est choisie de telle manière que OA=(mg)/k
Un dispositif non représenté ici permet d'éviter tout contact entre l'élastique et le support circulaire. On néglige les frottements de la perle sur le support.
Ainsi, on nous demande de projeter les forces qui sont appliquées au point M dans la base polaire mais je suis bloqué sur la projection de la tension de l'élastique. En prenant en compte la simplification de l'énoncé, je trouve :
T=-kxcos(θ).u(r)+kxsin(θ).u(θ)
Bonjour
Ce que tu note x est l'allongement de l'élastique que tu peux exprimer en fonction de l'angle theta et des autres caractéristiques du dispositif.
La seule décomposition de x que je vois de possible, c'est en utilisant la relation de Chasles MA=MO+OA mais je ne comprends pas comment on pourrait y introduire l'angle.
Ce que tu notes r =OM est noté 
sur le schéma. Il faut harmoniser.
Si on note 
l'angle entre AO et AM, exprimer h (hauteur du triangle de sommet M de deux façons différentes conduit à :
r.sin(
)=L.sin()
De plus :
OA=(m.g)/k=r.cos()+L.cos()
Selon l'énoncé, la longueur à vite de l'élastique est négligeable de sorte que la norme de la tension puisse s'écrire :
T=k(L-Lo)
k.L
N'y a-t-il pas par hasard d'autres approximations autorisées par l'énoncé ? r très petit devant OA par exemple ?
Bonjour,
Une simple remarque et je m'éclipse : la projection de T sur et
ne fait pas intervenir
. Ecrit vectoriellement avec un produit scalaire, cela doit se simplifier.
Quel est l'angle entre les vecteurs MA et ur si ur désigne le vecteur unitaire dirigeant OM ?
Ensuite : L.sin() et L.cos() peuvent s'exprimer en fonction de (m.g)/k, r et .
En considérant les angles orientés de sorte que et soient positifs sur la figure, tu as tout simplement :
En écrivant : tu obtiens par projection :
En développant le cosinus et le sinus de la somme et en tenant compte de mes messages de 12h35 et 13h48, tu obtiens les expressions relativement simples de Tr et T
.
Si tu n'es pas à l'aise en trigonométrie, une autre méthode (peut-être celle à laquelle pensait gts2...) te paraîtra peut-être plus simple :
Tu exprimes dans la base cartésienne les vecteurs
,
et
. Ensuite, par définition du produit scalaire :
Je vois, c'est assez simple en fait. Je pense que j'ai été bloqué surtout par cet angle ᵠ que l'on doit soi-même introduire. Je vous remercie beaucoup.
la FAQ du forum
moteur de recherche
page de choix du forum
fiches du site
Annuler
connectez vous