Inscription / Connexion Nouveau Sujet
Plan incliné en mouvement - Mécanique analytique
Bonjour, j'ai un exercice de mécanique analytique mais je bute sur 2 questions.
Voici l'énoncé :
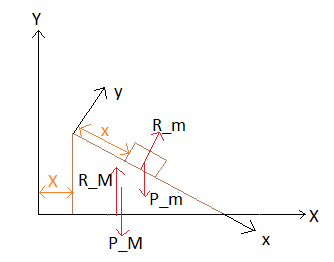
On considère une masse glissant sur un plan incliné non fixe sans frottement. On note M la masse du plan incliné et m la masse du mobile. L'angle est défini par les axes
est défini par les axes et
On note par
l'accélération de m relatif au plan incliné et
l'accélération du plan incliné, qui ne se déplace que selon
(voir schéma ci-joint).
1/ Déterminer les équations du mouvement par le PFD
2/ Déterminer les équations du mouvement par le PTV (principe des travaux virtuels) en dynamique
3/ Déterminer les équations du mouvement par le Lagrange.
Ce que j'ai fait :
On a ici 2 degrés de libertés qui sont x et X.
J'ai fait la méthode par Lagrange, je trouve à la fin 2 équations :
Mais je bloque pour les 2 autres questions (Newton et PTV en dynamique).
Pour la question 1, ce que j'ai fait :
On a avec
l'accélération d'entrainement de m et
l'accélération relative de m.
.
On a qui fait le lien entre le mobile et le plan incliné et a pour composante dans la base (O,X,Y) :
On peut donc écrire le PFD :
Ecrivons de même le PFD du mobile dans (0',x,y) : (composante selon x) et mg*sin(
 ) la composante du poids dans la direction x
) la composante du poids dans la direction x
Mais je bloque pour la suite.
Pour la méthode avec le PTV, je sais que (dans le cadre de ce problème) avec Fc les forces de contraintes et d
le déplacement élémentaire. On a donc ici 2 forces de contraintes : RM et Rm
Bien cordialement
Bonsoir
Je réponds pour l'instant sur le PFD appliqué dans le référentiel galiléen du laboratoire. L'accélération d'entraînement de la masse m est :
Les deux seules forces appliquées au solide de masse m sont le poids et la réaction normale du plan incliné. En projetant le PFD sur l'axe dirigé par puis sur l'axe dirigé par
on obtient :
Je te laisse appliquer le PFD à la masse M. N'oublie pas le principe des actions réciproques : si le solide de masse M exerce sur le solide de masse m la force , le solide de masse m exerce sur le solide de masse M la force opposée
. Tu devrais t'en sortir avec cela...
oui ! Il te reste à remplacer Rm par l'expression que je t'ai fournie précédement et tu auras directement l'expression de
Cela te permets ensuite d'obtenir l'expression de
Tu pourras alors vérifier que ces expressions des deux accélérations sont compatibles avec ton travail sur la méthode de Lagrange.
En remplaçant Rm par dans
, on a
Mais je vois pas de lien entre et
mis a part
=
mais cela ne m'amène pas à la bonne équation
Pour avoir l'accélération de la masse pm, il suffit de remplacer
On retrouve bien la même chose (j'avais fais une erreur de signe dans mon isolement de .
Reste désormais la méthode avec le PTV. Voici ce que je sais :
or ici on a 2 forces de contraintes : Rm et RM.
correspond au déplacement virtuelle
Post croisé !
Pour la méthode utilisant le PVT, je ne sais pas trop comment t'aider car il y a plusieurs façons de le présenter.... De toutes les façons, il faut tenir compte des quantités d'accélérations.
Personnellement, j'aurais tendance à utiliser le PVT d'abord pour le système constitué des deux masses. La seule force qui travaille est le poids de m.
On peut ensuite l'appliquer à la masse m seule.
On a donc (Principe d'Alembert)
On a ici juste une seul force qui travaille :
Il me manque plus que de trouver mais je n'arrive pas à le trouver. Je sais juste qu'il doit rendre compatible les forces de liaisons.
Bonjour
Petite étourderie dans ta dernière expression de l'accélération de m ; je rectifie :
Imagine un déplacement virtuel selon des deux masses. Le vecteur poids est perpendiculaire à ce déplacement et donc ne travaille pas. On obtient donc :
Je te laisse montrer que cela conduit à la seconde équation que tu as obtenue par la méthode de Lagrange :
Imagine maintenant un déplacement virtuel selon ; seule m peut subir un tel déplacement compte tenu du plan horizontal sur le quel glisse le solide de masse M:
Je te laisse vérifier que cela conduit à la première relation obtenue par la méthode de Lagrange ; c'est aussi le projeté suivant du PFD appliqué au solide de masse m.
Merci beaucoup.
Si j'ai bien compris, faut prendre un déplacement virtuel qui est perpendiculaire aux forces de liaison afin que le produit scalaire de cette force par ce déplacement soit nul ?


