Niveau licence

Plan incliné,dynamique du point

Posté par
Jean469 23-04-15 à 20:54

Bonsoir,je dois faire cet exercice en mécanique mais je voulais savoir si mes réponses sont bonnes:
Le voici:
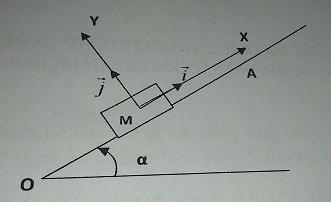
Un mobile M de masse m est assujetti à glisser avec frottement sur un plan incliné faisant un angle $\alpha$ avec l'horizontale .

Il est lancé vers le haut à $t_0=0$ avec une vitesse initial $\vec{v}= v_0.\vec{i}$ depuis le point O d'abscisse x=0.
Il est ainsi soumis à une force de frottement k(k est une constante de frottement $\vec{f}=k.\vec{R_N}$ .

Après que sa vitesse se soit annulée en A,à cause des frottement et de la pesanteur,il redescend.

A)Étude de la montée.

Après avoir effectué le bilan des force exercées sur le mobile M,écrire la relation fondamentale de la dynamique permettant d'obtenir les équations différentielles du mouvement (cad les composantes de l'accélération suivant $\vec{i}$ et $\vec{j}$ .

2)En déduire les expressions des vecteurs vitesse $\vec{v}$ et position $\vec{OM}$ du mobile M.

3)A quel instant t_a le mobile s'arrête-t-il en A?

4)En déduire la distance x_a parcourue par le mobile M lors de la montée.
J'aurai posté une photo du schéma ou dessiner le schéma,mais c'est interdit je crois.

Néanmoins,j'ai pu dire:

1)Le bilan des forces est le suivant:Le poids $\vec{P}=m.\vec{g}$ ,la force de frottement $\vec{f}=k.\vec{R_N}$ .

Et on sait que $\sum \vec{F_i}=m.\vec{a}$ .
Donc $\vec{f}+\vec{P}=m.\vec{g}+k.\vec{R_N}=m.\vec{a}$ .

Puis on remarque que la projection suivant $(O_x)$ donne $a_x=\frac{k.R_N}{m};(m.a_x=k.R_N)$ .
.... $(O_y)$ donne: $a_y=-g+\frac{k.R_N}{m};(m.a_y=-mg+k.R_N.$

Par conséquent, $v_y= \int {a_y}=\int -g+\frac{k.R_N}{m}=-gt+\frac{k.R_N.t}{m}.$

Et $v_x= \int {a_x}=\int \frac{k.R_N.t}{m}.$

Donc $x=\int {v_x}=\int \frac{k.R_N.t}{m}=\frac{k.R_N.t^2}{2m}$ et $y=\frac{-gt^2}{2}+\frac{k.R_N.t^2}{2m}. \\$

Donc $\vec{v}=v_x.i+v_y.j$ i,et j deux vecteurs.

Et $\vec{OM}=x.i+yj$ .

3)Le mobile s'arrête en A quand $\vec{v}=0$ ,quand $v_a=0$ ,donc quand $v_x.i+v_y.j=0$ .

De plus on sait qu $t_a=\frac{x_a}{v_a}$ . $x_a$ ou $d_a$ .
donc $x_a=v_a.t_a.$

Posté par re : Plan incliné,dynamique du point 23-04-15 à 22:28

bonsoir,

vous pouvez tout à fait poster des schémas (même scannés) comme je viens de le faire ci-dessous
ce qui est interdit c'est de scanner le texte des énoncés

vos projections sont à revoir car vous ne tenez pas compte de la pente!
d'autre part R_N a une projection nulle sur (Ox) (cf dessin)
et il ne faut pas oublier f

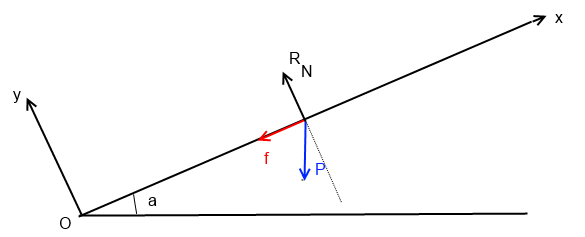
Plan incliné,dynamique du point

Posté par re : Plan incliné,dynamique du point 23-04-15 à 22:39

autre chose: le vecteur f n'est pas colinéaire à R_N

on a |f| = k |R_N|
mais vectoriellement on a: f = -k |R_N|
(en cas de glissement, f est toujours dans le sens inverse de la vitesse de glissement)

Posté par re : Plan incliné,dynamique du point 24-04-15 à 00:05

Ah merci,ça m'aide bien parce que sur mon schéma que voici:

Plan incliné,dynamique du point

Je n'étais pas sûr de l'endroit ou je mettais $R_N$ ^^.
Bon et bien je vais travailler avec ces information .

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !

Posté par re : Plan incliné,dynamique du point 24-04-15 à 09:34

La projection des forces sur l'axe Ox permet d'écrire instantanément l'équation différentielle demandée au début.

mg.sin(a) + k.m.g.cos(a) = - m.dv/dt

dv/dt = - g.(sin(a) + k.cos(a))

v(t) = Vo - g.(sin(a) + k.cos(a)).t

Le mobile a une vitesse nulle pour tA tel que : Vo - g.(sin(a) + k.cos(a)).tA = 0
tA = Vo/[g.(sin(a) + k.cos(a))]

v(t) = dx/dt

x = S (Vo - g.(sin(a) + k.cos(a)).t) dt
x = Vo.t - g.(sin(a) + k.cos(a)).t²/2 + K
x(0) = 0 --> K = 0

x(t) = Vo.t - g.(sin(a) + k.cos(a)).t²/2

x(tA) = Vo²/[g.(sin(a) + k.cos(a))] - g.(sin(a) + k.cos(a)).Vo²/[g.(sin(a) + k.cos(a))]² /2

x(tA) = Vo²/[g.(sin(a) + k.cos(a))] - Vo²/[2g(sin(a) + k.cos(a))]

x(tA) = Vo²/[2g.(sin(a) + k.cos(a))]
-----
Sauf distraction.

Posté par re : Plan incliné,dynamique du point 26-04-15 à 22:13

Merci beaucoup pour ces explications détaillées J-P
Je viens de voir ton message

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Plan incliné,dynamique du point

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique