Inscription / Connexion Nouveau Sujet
Plan de symetrie électromagnétisme
Bonjour tout le monde,
Pour une distribution linéique de courant sur un fil infini, tout plan passant par un point M et le fil est un plan à la fois de symétrie est d'anti-symétrie pour la distribution de courant ( car elle est nulle en dehors du fil). Donc le champ B est à la fois orthogonale est appartenant à ce plan ??
Bonjour
Revois bien ton cours sur la notion de plan de symétrie et sur la notion de plan d'antisymétrie pour une source de champ magnétique. De l'aide si nécessaire, ici, paragraphes III et IV : ![]()
Dans le cas qui t'intéresse : le plan contenant M et le fil est plan de symétrie, donc le vecteur champ B en M est orthogonal à ce plan.
Le plan contenant M et orthogonal au fil est plan d'antisymétrie : le vecteur B en M appartient donc à ce plan ; ce résultat est cohérent avec le précédent mais moins précis puisqu'il ne permet pas d'obtenir, contrairement au raisonnement précédent : en coordonnées cylindriques.
Pouvez vous me dire pourquoi il n'est pas un plan d'anti-symetrie ?
ce plan divise la distribution de courant en deux : l'une =+0 et l'autre =-0
c'est donc bien un plan d'anti-symetrie non ?
ce plan divise la distribution de courant en deux : l'une =+0 et l'autre =-0
Je ne suis pas sûr que tu aies bien compris la notion de plan de symétrie ou d'antisymétrie dans le cas où la source est caractérisée par un vecteur (vecteur densité de courant) et non pas par une grandeur scalaire algébrique (charge électrique ou masse). Revois bien le document dont je t'ai fourni la référence. Pour t'aider dans le cas particulier où la source est un conducteur cylindrique de longueur infinie, tu peux t'intéresser aux schémas ci-dessous.
Celui de gauche a pour plan de figure le plan contenant M perpendiculaire au fil : le plan
Un jour de contrôle, ce résultat définit complètement la direction du vecteur champ ; tu peux passer aux étapes suivantes : étude des invariances de la source puis application du théorème d'Ampère.
A titre d'information complémentaire, je te fournis le schéma de droite : le plan de figure est maintenant le plan contenant M et l'axe (O,z) du conducteur cylindrique. Le plan contenant M et perpendiculaire à (Oz) (plan
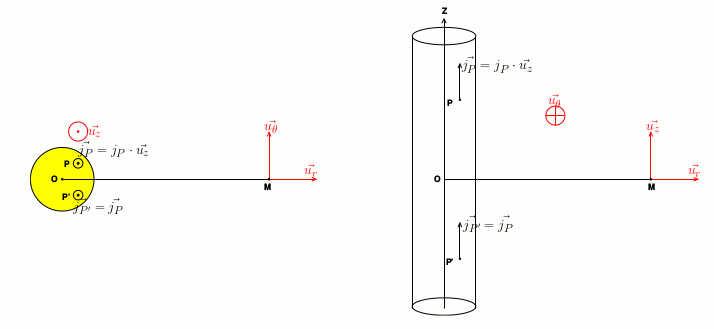
Vous avez considerer une distribution volumique ( cylindre ) de courant, mais moi j'ai considérer une distribution linéique ( fil )
Le cas linéique est une approximation permettant, dans les calculs, de considérer le rayon du cylindre très petit devant la distance r=OM. Cela ne change rien aux symétries et aux invariances de la source. Surtout : il faut raisonner sur des vecteurs, pas des grandeurs scalaires algébriques.
Ah ! Je viens de comprendre, merci beaucoup. En effet, vous avez raison, la symétrie des grandeurs vectorielles n'est pas la même que pour les grandeurs scalaires où il suffit d'ajouter un signe - . Merci encore Vanoise.



