Inscription / Connexion Nouveau Sujet
Pile & fém
Bonjour 
J'ai un petit exercice que je n'arrive pas à résoudre.
Cette pile est réalisée en milieu basique (voir plus bas).
1) Faire un schéma de cette pile.
2) Ecrire la réaction de fonctionnement.
3) Montrer que la fém est indépendante de la concentration c.
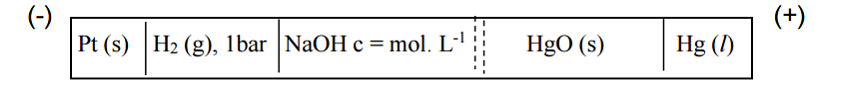
Alors :
1) (-) Pt|H2, 1 bar|NaOH, c|HgO(s)|Hg(l) (+)
Pour le schéma, ça ne devrait pas poser de quelconque problème :
D'un côté, nous avons un bac de NaOH avec l'électrode à hydrogène (anode).
De l'autre, nous avons un bac de la solution acide avec l'électrode de Platine (cathode).
Les deux sont reliées.
Ensuite, ça se corse.
Nous avons une oxydation à l'anode ; couple OH-/H2
H2+2H2O=2OH-+2e-+4H+
Je me doute que je doive me servir de la relation de Nernst mais bon, je bloque.
Merci d'avance.
Pour l'équation générale de fonctionnement, il faut écrire les 2 équations des demi-réactions et les additionner de façon à faire disparaître les électrons !
2) H2+2H2O=2OH-+2e-+4H+
HgO(s)+2e[sup]-[/sup]+2H+=Hg(l)+H[sub]2[/sub]O
H2+HgO(s)=Hg(l)+H[sub]2[/sub]O ??
Dans mon équation générale ? L'eau est présente non ? Mes yeux me joueraient-ils des tours ? Et puis l'eau n'est pas forcée d'intervenir, en général si ni des HO- ni des H+ ne sont présents, l'eau ne joue aucun rôle particulier, à part de solubiliser les composants...
Regarde le Sodium il est là mais se contente de regarder tous ces ions en mouvements sans intervenir.
Je pense qu'il faut faire E=E2-E1=E°2+0.03logP(H2)=E°2 donc
Comme c'est indépendant du pH donc de la concentration ?
En fait il faut exprimer [HO-] en fonction de [H+] dans ton E2 et normalement les [H+] vont se simplifier quand tu fais ton E2 - E1 et le tour est joué !
En fait il faut exprimer [HO-] en fonction de [H+] dans ton E2 et normalement les [H+] vont se simplifier quand tu fais ton E2 - E1 et le tour est joué !
Comment le faîtes-vous ? D'ailleurs, je n'ai jamais compris pourquoi E°1 était nul.
Tu as la formule valable partout, tout le temps et dans tous les cas à 25°C : [H+][HO-] = 10-14 !
Pour [HO-] c'est réglé.
Et après E°1 est nul car on ne sait mesurer que es différences de potentiel, donc il nous faut une référence : alors on choisit E° (H+ / H2) = 0 par convention. C'est une convention en fait. Toujours ce E° sera nul pour ce couple !
Donc :
A partir de là, je suis réellement bloqué... Je sais que ce ne sont que des questions de maths pourtant.
Donc comme je t'ai dit tu peux éradiquer le [HO-] (et tu le dois :p ) comme ça tu as du [H+] partout et après tu utilises les règles de calcul des log pour éliminer les [H+].
Hé bien non en fait il ne faut pas faire disparaître le [HO-] mais le calculer en fonction de [H+] avec la formule [H+][HO-] = 10-14. Après les [H+] devraient se simplifier par le calcul.
Le milieu étant basique, je crois que tu as intérêt à équilibrer les demies réactions avec des ions hydroxyde.
demie pile n° 1 :
demie pile n° 2 :
L'équation bilan de la réaction de fonctionnement est ainsi :
La f.é.m. de la pile vaut donc :
Avec P° = 1bar : pression standard. Cette expression ne fait pas intervenir la concentration en ions hydroxyde ou en ions oxonium, elle est donc indépendante du pH : logique puisque l'équation bilan ne fait intervenir aucun de ces deux ions !
Attention : les potentiels standard des couples correspondent avec cette convention d'écriture à l'état standard de l'ion hydroxyde (pH = 14) et non, comme souvent, à l'état standard de l'ion oxonium (pH=0) : cela n'est pas gênant : les deux demies réactions faisant intervenir le même nombre d'ions hydroxyde la différence de potentiel standard entre le cas pH = 0 et le cas pH = 14 est le même : la différence est donc la même quelle que soit la convention d'écriture.
Merci à tous les deux pour toutes ces explications et précisions.
vanoise, comment obtenez-vous dans la fém le terme en log ?
comment obtenez-vous dans la fém le terme en log ?
Formule classique de Nernst sans faire l'hypothèse simplificatrice consistant à écrire que la pression partielle de dihydrogène est égale à la pression standard.
Complément à ma remarque précédente : le mercure et l'oxyde de mercure sont deux corps purs seuls dans leurs phases, phase liquide pour l'un, phase solide pour l'autre : leurs activités sont toutes deux égales à l'unité : ils n'interviennent pas dans l'équation de Nernst : faire intervenir la concentration en mercure est donc une grosse erreur !
faire intervenir la concentration en mercure est donc une grosse erreur !
Oh oui évidemment !! Autant pour moi j'en suis désolé !
Complément à ma remarque précédente : le mercure et l'oxyde de mercure sont deux corps purs seuls dans leurs phases, phase liquide pour l'un, phase solide pour l'autre : leurs activités sont toutes deux égales à l'unité : ils n'interviennent pas dans l'équation de Nernst : faire intervenir la concentration en mercure est donc une grosse erreur !
D'accord, je comprends mieux ! Cependant, pour le mercure et son oxyde, je ne pouvais pas le savoir, mon prof n'en a jamais parlé. Il y a d'autres espèces de ce genre ?
faire intervenir la concentration en mercure est donc une grosse erreur !
Oh oui évidemment !! Autant pour moi j'en suis désolé !
Pas de soucis, merci à vous deux de prendre autant de temps pour m'aider !

Cependant, pour le mercure et son oxyde, je ne pouvais pas le savoir, mon prof n'en a jamais parlé. Il y a d'autres espèces de ce genre ?
En fait si c'est marqué sur le schéma de la pile : une est solide l'autre gazeuse : tu connais donc leurs activités !
Ah, j'avais mal compris.  Je pensais que le mercure était un peu comme l'eau, une espèce un peu à part si je puis dire.
Je pensais que le mercure était un peu comme l'eau, une espèce un peu à part si je puis dire.
une est solide l'autre gazeuse
Mea culpa : une est LIQUIDE l'autre l'autre SOLIDE ! Décidément !
une espèce un peu à part si je puis dire.
Oh elle l'est ! C'est un métal liquide aux conditions normales de pression et de température ! Mais ici en effet c'est au niveau des activités qu'il faut raisonner et donc regarder les états des espèces en présence.


