Je m'excuse , d'avoir fait une erreur dans mon premier message. Et d'avoir fait du plagiat.

Lionel

Bonsoir,

Je pense que tu as oublié de poster les questions, en plus de l'énoncé de l'exercice.

1. As-tu fait un schéma de la situation ?
2. Ensuite, oui, le théorème de l'énergie cinétique pourrait s'avérer utile pour déterminer la vitesse finale.

Bonjour ,

Tout d'abord merci d'avoir commencé à m'aider pour ce problème. L'énergie cinétique s'appliquerait mais il y a la force de frottement que je ne sais pas quoi faire avec. J'ai fait un shéma en indiquant les principales  force cependant j'ignore si je dois ajouter une accélération pour ce problème.
J'ai supprimé du problème les 2 premières questions.( culculer la force de traction à la montée et faire un shéma.)Mais si vous voulez je peux rajouter ces données en entier.

Merci pour votre aide.

Lionel

Il faut toujours poster un énoncé complet et présenter tes pistes sur les questions résolues ...

Ensuite, ça serait bien que tu postes le schéma en question.

Pour l'application du théorème de l'énergie cinétique, tu as la valeur de la force de frottement, donc exprimer le travail de chaque effort sur le parcours ne pose pas de difficulté.

Bonsoir ,

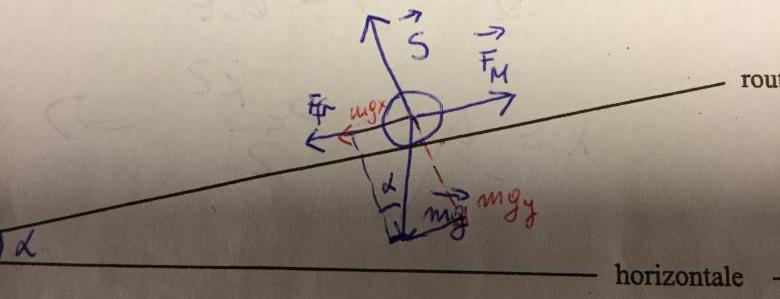
Je vous est attaché une pièce jointe comportant le schéma en question.  Pour ce qui est des forces si j?obtiens la Force motrice. Est-ce que ça pourra m?aider à trouver la vitesse?

Je vous remercie de m?aider à comprendre ce problème.

Lionel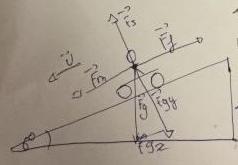



***Image recadrée***

Bonjour ,

Je crois  mieux comprendre ce problème cependant nous n'avons pas encore vu l'energie cinétique en classe. Ce devoir était censé porté uniquement sur les forces de Newton. Pourriez-vous m'ecrire le théorème pour que je puisse essayer de trouver la vitesse.

En vous remerciant encore de votre aide.

Lionel

Salut,

Alors :

[lien]

=> cette fiche rappelle la notion de travail d'une force.

[lien]

=> celle-ci la notion d'énergie cinétique et le théorème à appliquer dans cet exercice.

Bonsoir ,

J'ai appliqué dans le théorème mais il me manque quelque chose.  M=70kg

1/2*70*v^2=somme des forces
1/2*70*v^2= -10+10-20 (réaction, gravité et frottement )
Au final je ne trouve pas de réponse pour v. Quand je fais la racine carré le nombre étant négatif donne aucune réponse.

Pourriez-vous me dire si il s'agit de la bonne formule?

Et merci pour vos fiches qui m'ont beaucoup aidé.

Lionel

Alors,



= vitesse initiale du cycliste = 0 m/s ;
= vitesse finale recherchée.

= poids du cycliste ;
= réaction normale de la route ;
= réaction tangentielle = force de frottement.

La direction de la réaction normale de la route étant perpendiculaire au déplacement AB, elle ne travaille pas :

Finalement, on peut écrire :

Bonsoir ,

La force de frottement est-elle négative ou positive ?

Merci pour cette explication très précise.

Lionel

Oui,

Bonsoir ,

Je me donne à fond pour le résoudre et comprendre et j'obtiens une réponse irréaliste.
A la fin je divise ce total par un nombre pour isoler v au carré puis j'applique la racine carré et j'obtiens comme réponse v=169
Est-ce que je dois appliquer une formule pour convertir 169.
Je vous est attaché la façon par laquelle j'ai remplacé la formule.

Merci

Lionel

** image supprimée **

Salut,

Pas de scan, tu as tous les outils pour taper tes pistes.

Concernant tes calculs, un résultat sans unités c'est 0 le jour d'un examen.

Ensuite, je pense que le problème vient de la notion de déclivité.

En effet, si je me fie à ce site, une déclivité de 6% ne conduit pas à un angle de 10° :

Bonjour ,

Je l'ai résoud en remplacant les termes de la formule , je pense me tromper à la fin ou alors je dois faire une autre formule.
Alors selon la vitesse que j'ai trouvé. V=47 [m/s ]et un temps = 31 secondes. Est-ce possible comme réponse ?
Je vous joins mon raisonnement.

0.5*mv^2=-Ff*AB+m*g*h (hauteur)
0.5*70*v^2=-20*1500+70*10*156
35v^2=79200
v^2=2262
v=47.5[m/s]

Merci

Lionel

Déclivité = 6% = sin(alpha)

Wab(P) = m*g*AB*sin(alpha) = 70*10*1500*0,06 = 63 000 J
Wab(Rt) = -Rt*AB = - 20*1500 = -30 000 J (négatif car travail résistif)
Wab(Rn) = 0 J (ne travaille pas car perpendiculaire au déplacement)

donc Wtot = 63 000 - 30 000 = 33 000 J

1/2*m*v² = Wtot

<=> v = (2*Wtot/m) = (2*33 000/70) = 30,7 m/s

soit v = 110 km/h

Tu peux remarquer la limite du modèle. Dans les faits, la force de frottement d'un système n'est pas constante, d'autant plus quand la vitesse augmente et devient conséquente.
En effet, les forces de frottement fluide exercées par l'air sur le système ne sont pas prises en compte ici, alors qu'elles auraient tendance à ralentir davantage le cycliste.

Tout d'abord , j'aimerais vous remercier de votre aide. Pour moi ce chapitre me paraît beaucoup plus clair. Sinon j'ai une question sur votre développement.
Mon sinus de l'angle est différent.
Sin=Opposé /hypoténuse
1500sin (6°)=opposé
156.8 = opposé ?

Merci encore

Lionel

Tant mieux si tout te semble plus clair, c'était mon objectif de reprendre l'exercice et les parties du cours au pas à pas.

Concernant ton calcul de l'angle, en fait c'est inutile de le faire dans cet exercice.

D'après le lien que je t'ai fourni, la déclivité correspond au sin de l'angle.

Or si je calcule le travail du poids sur AB, le produit scalaire du "vecteur" poids par le "vecteur" déplacement conduit au sinus de l'angle alpha, soit directement le 6% = 6/100 = 0,06.

D'où mes calculs .

Je te conseille de t'entraîner sur le calcul des produits scalaires. Sinon, tu sembles avoir compris l'exercice et l'application du th de l'énergie cinétique

Bonsoir ,

Je ne sais pas si une fois le problème résolu vous notez ' Résolu '.

Recevez mes meilleures remerciements.

Lionel

Je t'en prie .

Cet échange pourra servir à d'autres, on ne clôture donc pas le topic.

A+

Bonjour ,

Je vous informe que dans le problème on ne devait pas utiliser le scalaire mais simplement trouver la hauteur (156.8 m). La vitesse est de 40.7 m/s.
On peut résoudre par le théorème mais aussi en cherchant accélération par force de pesanteur de x.  Le scalaire est utilisé pour les angles. Je cite ma profe.

Merci de l'aide et du forum qui m'a permis de m'enrichir.

Lionel

Bonjour Lionel,

Je n'ai fait qu'appliquer la définition d'un travail d'une force puis le théorème de l'énergie cinétique :

En effet, le travail d'une force constante pour un déplacement rectiligne (ce qui est le cas dans ton exercice) de son point d'application est le produit scalaire de par .

Effectivement, par une relation de Chasles, tu peux revenir à une autre présentation du travail du poids : W_AB(P) = m*g*(za - zb) que ta prof souhaitait que tu appliques directement. Mais appliquer l'une ou l'autre revient au même résultat final :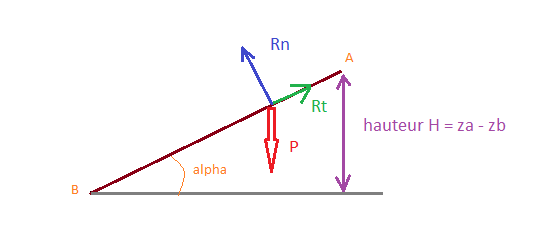



Si j'utilise les mathématiques dans le triangle rectangle dessiné ci-dessus :

sin(alpha) = H/AB = (za - zb)/AB

soit H = AB*sin(alpha) = L*sin(alpha) en accord avec les notations de ton énoncé.

Donc W_AB(P) = m*g*L*sin(alpha).

On en revient donc à ce que j'avais écris pour le poids du solide dans mon message du 30-10-17 à 13:17.

C'est donc étrange qu'on n'arrive pas au même résultat.

Soit j'ai fait une faute d'inattention dans mon application numérique, soit on n'a pas la même définition de la déclivité = 6% = sin(alpha) ...

C'est toujours sympa d'avoir un retour suite à une aide.

Bonne fin d'après-midi.

Bonjour,

Somme F =m*a
-Ff + Fgx = m*a
-20 + 70 *10*sin(6)= 70*a
a=53,17/70
a=0.76[m/s^2]

X=0.5*at^2+vot
1500=0,5*0.76*t^2
1500/0.38=3949,6
Racine carré de 3949.6 donne 62,8 [s]

a= delta v/ delta t
a*delta t = delta v
0,76*62,8= 47,7[m/s]

Ceci est l'explication de ma prof de physique.
Merci de m'aider.

Lionel

-Ff + Fgx = m.a
-20 + 70 * 10 * 0,06 = 70.a
12 = 70.a
a = 22/70 = 0,314 m/s²

X = 0,5.at² + Vo.t
1500 = 0,5 * 0,314 * t² + 0
t² = 9554
t = 97,74 s

vf = Vo + a*t
Vf = 0 + 0,314 * 97,74 = 30,7 m/s

... Et bien entendu, on retrouve la valeur trouvée par gbm par la méthode utilisant le théorème de l'énergie cinétique
------------


Une déclivité de 6 % ne signifie absolument pas que l'angle fait par la route avec l'horizontale est de 6°

Et donc la ligne : -20 + 70 *10*sin(6)= 70*a (qui veut dire pour toi -20 + 70 *10*sin(6°)= 70*a) est tout à fait fausse.
----
Une déclivité de 6 % signifie que la route s'élève de 6 m par 100 m parcourus sur la route.

Hello J-P

il me semble que le % indique la tangente plus que le sinus. Ceci étant tu as raison de souligner que 6° n'est égal à 6% quand dans la bière ... ou le vinaigre

Bonsoir ,

Fp= m*g

Voici un schéma qui détaille plus la force de pesanteur.
Merci @Dirac d'avoir trouvé le problème.

Lionel

Voilà le schéma

Bonsoir à tous,

@J-P : si on retrouve le même résultat avec deux méthodes différentes, c'est de bon augure .

@Dirac et Lionel : tout comme J-P, je pense malheureusement que c'est le professeur de Lionel qui s'est planté ... En effet, c'était bien le terme "déclivité" qui était précisé dans l'énoncé (qui fait écho au sinus de l'angle formé avec l'horizontal) et non "pente" (qui fait écho à la tangente de l'angle formé avec l'horizontal).

Lisez ceci :

Attention à ton dernier schéma, il n'y a que 3 efforts appliqués sur le cycliste lorsqu'il se laisse descendre en roue libre : force de frottement, poids du cycliste et réaction normale du support.

Que le prof de Lio se soit planté était clair pour moi,

Par contre, je pensais à mon âge que pente et déclivité étaient synonymes ... eh ben j'aurais appris quelque chose.

Merci J-P, merci gbm ,   je me coucherai (un peu) moins bête

(tout ça parce que je voulais caser la blague 6° = 6% dans la bière uniquement)

Bonsoir

C'est ma faute la pente est de 6 °  et pas de 6 pourcent.

Si on fait 6 pourcent vous avez raison et si on fait 6 ° j'ai raison.

Merci et cela prouve que je dois être plus précis concernant les données des exercices.

Lionel

Double emploi.

Ce faisant, comme tu as pu le lire sur le lien, "pente" et "déclivité" coïncident pour de petits angles, mais au-delà de 6° (à ne pas confondre avec 6% Lionel ), c'est déjà moins vrai.

Après Dirac, si tu as envie d'une petite bière à 6% = 6°, rien ne t'empêche de la boire

-----------

Ce qui m'embête dans tout ça, c'est que le professeur induise Lionel en erreur ...

L'intérêt de nos échanges est que tu auras eu deux méthodes possibles pour arriver à tes fins. A toi de choisir celle que tu préfères :
* théorème de l'énergie cinétique (cf. mes messages du 30-10-17 à 13:17 et 06-11-17 à 17:07) ;
* deuxième loi de Newton (cf. message de J-P du 06-11-17 à 17:48).

Tu as été plus rapide que moi J-P.

Désolé pour l'explication redondante.

Bonsoir

Je vais regarder avec ma prof de physique car vous avez raison. Je n'ai pas très bien compris la fiche qui explique déclivité mais je vais m'instruir sur ce thème.
Merci de vos aides précieux.

Lionel

Bonjour ,

Si  100pourcent = 90degré
6 pourcent = 5,4degré

C'est la règle de trois.
Donc l'angle n est pas 0,06.

Lionel

Bonjour Lionel,

Tu confonds de nouveau la valeur de l'angle (exprimée en °) avec la déclivité (exprimé en %).

6% = 0,06 = sin(alpha) => alpha = Arcsin(0,06) = 3,44° comme J-P te l'as déjà écrit dans son message du 06-11-17 à 19:20.

De manière générale, le sujet a entièrement été abordé dans nos échanges.

Laisse-toi le temps de décanter tout ça, en particulier sur trois points majeurs :

* le bilan des forces lorsque le cycliste est en roue libre (première faute d'inattention d'après ton schéma) ;

* différence entre la déclivité de 6% = 0,06 = sin(alpha) et la valeur de l'angle alpha fait avec l'horizontale = Arcsin(0,06) = 3,44° ;

* l'application du théorème de l'énergie cinétique (ma méthode) et de la deuxième loi de Newton (méthode de J-P).

Bonsoir ,

J?ai compris voilà un site qui prouve l?exactitude de l?angle ;


Je parlerai à ma prof.

Merci encore

Lionel

Ton lien ne parle que de la pente ... mais pas de la déclivité.

Sur ce lien :  , les 2 notions sont expliquées.

Bonjour
Elle est d'accord qu'elle s'est trompé mais elle m'a dit arctan (0,06
Est-ce vrai ou j'ai raison de faire arcsin(Alpha

Lionel

Bonjour,

On fait en 1 arctan(6/100)=3,43
En 2 sin(3,43)=0,06

Là est-ce juste ?

Lionel

Salut à tous,

Rien à ajouter aux propos de J-P.

Moi non plus

Et même ... si je pouvais en retirer ...

Bonjour ,

Je vous remercie de m'avoir aidé ma prof a reconnu son erreur.

Merci à l'ensemble des participants  et je vous souhaite à tous de passer une excellente journée.

Lionel

Salut,

Parfait ! Affaire classée .

Je t'en prie,

A+