Inscription / Connexion Nouveau Sujet
Physique :les forces
Bonjour à tous j'ai une question concernant cette exercice pourriez-vous m'aider s'il vous plaît.
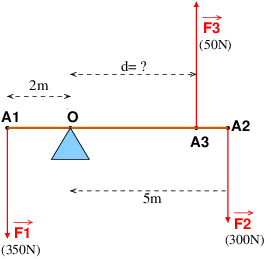
Une barre de 7m de long pivote autour d'un point situé à 2m extrémité gauche . Une force de 50N est appliquée à l'extrémité gauche et une force de 300 N est appliquée à l'extrémité droite de la barre . Ces deux forces sont verticale et dirigé vers le bas. A quelle distance du pivot une force de 200 N doit elle être appliquée pour assurer d'équilibre de rotation de la barre?
2m
3m
1m
4m
Je n'arrive pas à résoudre cette exercice quelqu'un peu m'aider
Merci d'avance
* mmalou > niveau modifié en fonction du profil renseigné *
L'énoncé n'est pas très clair. Il faut imaginer une barre pouvant pivoter autour d'un axe situé à 2m d'une extrémité. Il s'agit de trouver une condition d'équilibre c'est à dire une position ou la rotation ne se produit pas. De plus, il faut négliger le poids de la barre devant les autres forces.
Une barre, comme une tige possède toujours des dimensions transversales très petites devant la longueur. Elle peut être représentée par un trait épaisseur horizontal. L'axe de rotation est perpendiculaire au plan de figure. Tu le représente par un point. Reste à représenter les vecteurs forces et à appliquer le théorème des moments.
Tu dois écrire que la somme algébrique par rapport à l'axe de rotation des trois moments de force est nul.
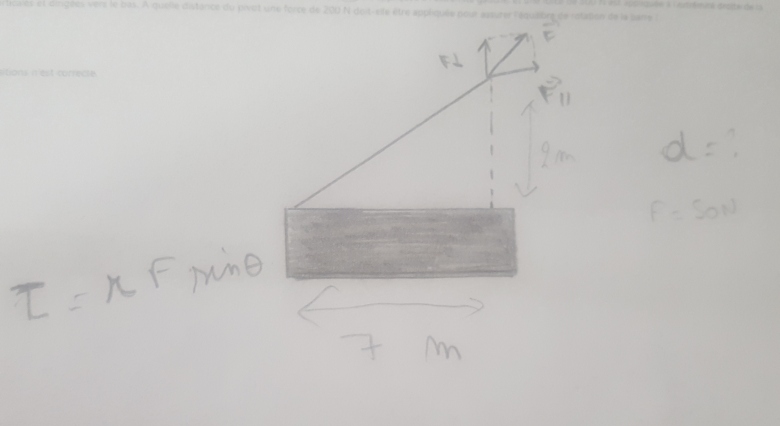
J'ai l'impression que tu n'arrives pas à te représenter la situation... Essaie de faire un schéma soigné avec les divers vecteurs forces. Cela n'a rien à voir avec la loi de Coulomb sur les frottements solides.
Calculs fait, je remarque que ton énoncé est faux. L'équilibre est impossible à réaliser avec une force appliquée à l'extrémité gauche aussi faible. J'ai donc remplacé 50N par 350N afin de tomber pour d sur une des valeurs proposées.
Je viens de réaliser une petite erreur sur mon schéma : je n'ai pas le temps de recommencer. F3=200N et non 50N