Bonjour Enae,

tu n'as pas fait d'erreur de raisonnement. Bien evidemment la vergence d'un miroir concave doit etre positive, puisque c'est un systeme optique convergent. Lorsqu'il y a un signe moins dans une relation qui devrait donner une quantite positive, c'est qu'il y a eu en amont une convention d'orientation...

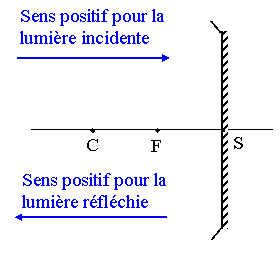
Traditionnellement on oriente l'axe optique selon le sens de parcours de la lumiere. Pour des systemes dioptriques (dioptres plans ou spheriques, lentilles etc...) pas de souci puisque la lumiere se deplace toujours dans le meme sens (gauche -> droite ou inversement). Pour des systemes catadioptriques (cad contenant une surface reflechissante), le rayon change de sens de parcours. Aussi, pour avoir des relations algebriques "universelles", cad convenant a chaque type de systemes, certains puristes ont adopte une double orientation de l'axe optique. Voir schema ci-dessous : pour tout ce qui concerne la lumiere incidente (objets, foyer objet), l'axe est oriente > 0 de gauche a droite ; pour tout ce qui concerne la lumiere reflechie (images, foyer image), il est oriente de droite a gauche...

La vergence d'un miroir spherique a alors la meme expression que celle d'une lentille mince : V = n_i/f_i = - n_o/f_o, ou no et ni sont les indices de refraction des milieux constituant l'espace objet et l'espace image respectivement, f_o et f_i etant les distances focales objet et image.

Pour une lentille, on peut imaginer que les milieux situes a sa gauche et a sa droite sont differents, d'ou la necessite de faire intervenir leurs indices ; sinon, si la lentille est utilisee dans l'air (c'est quand meme la majorite des cas), on obtient V = 1/f_i = - 1/f_o, meme resultat puisque f_o = - f_i. Bien entendu, pour un miroir spherique la distinction entre n_o et n_i n'a aucun sens : n_o et n_i sont identiques et on obtient V = 1/f_i = -1/f_o.
On peut montrer que pour un miroir f_o = SF_o = SC/2 (il y a des barres au-dessus des segments car ce sont des valeurs algebriques, pas faciles a faire donc je les remplace par des caracteres gras).

Bien sur, tu vas me dire que pour un miroir foyers objet et image sont les memes : oui, mais l'un appartient a l'espace objet donc il suit la convention d'orientation suivant le sens de la lumiere incidente, et l'autre appartient a l'espace image donc il suit la convention inverse...
Sur le schema ci-dessous on a :
*)  pour le foyer objet, F = F_o, F_oS > 0, donc SF_o = f_o < 0 ; V = -1/f_o est positif.
*)  pour le foyer image, F = F_i, SF_i = f_i > 0 ; V = 1/f_i est positif.

Tu verifieras toi-meme que pour un miroir convexe on arrive a la meme conclusion (V < 0).

Si ce n'est pas clair, ce n'est pas ma faute... cette double convention est une source inepuisable d'erreurs de signe et je ne l'ai jamais utilisee, et encore moins enseignee a mes etudiants : en physique, il y a suffisamment d'occasions de se planter dans les signes qu'il est inutile d'en rajouter. La bonne attitude est la tienne : quel que soit e choix de l'orientation de l'axe optique, la vergence d'un systeme optiqyue doit etre >0 s'il est convergent (cad si un rayon incident // a l'axe donne un emergent rabattu sur l'axe optique), negatice dans le cas contraire.

Prbebo.