Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

perte de charge

Posté par
iSirrol 27-11-16 à 16:36

bonjour

perte de charge
On souhaite brancher une conduite sur un réservoir. Plusieurs possibilités sont possibles, mais laquelle générera le moins de perte de charge ?

A B ou C ?

mon intuition me donnerai plutôt C mais je ne vois pas comment le justifier

Posté par
vanoisere : perte de charge 27-11-16 à 18:07

Bonjour
Tu as évidemment raison. Plus l'écoulement s'écarte du laminaire plus les pertes de charges sont importantes. Pour la théorie : tu peux t'intéresser à ce document sur les pertes de charges singulières. La figure 36 en particulier est très explicite.

Posté par
iSirrolre : perte de charge 27-11-16 à 18:09

Oui d'accord c'est assez intuitif

Posté par
iSirrolre : perte de charge 01-12-16 à 11:30

Je viens de lire le site que tu m'as envoyé plus en détail, et c'est intéressant on apprend plusieurs choses que l'on avait pas abordé de cette manière dans mon cours.

C'est très utile pour le dimensionnement de canalisation (dans le cas du remplissage d'un château d'eau en amont d'un lac par exemple).
perte de charge

La figure 36 m'a été très utile pour trouver le coefficient de perte de charge singulière K dans le cas d'un coude arrondi de 90° et de rayon de courbure R=375mm
K=\dfrac{1}{2}(0.131+1.847(\dfrac{D}{0.375})^{\frac{7}{2}})

Posté par
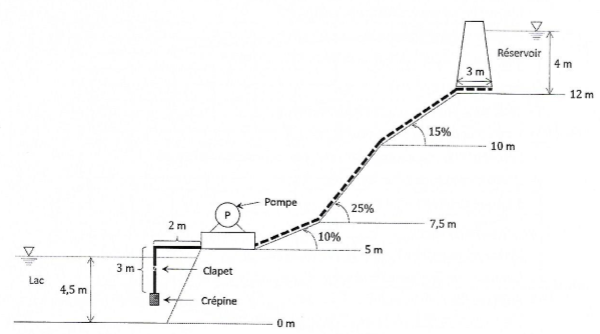
iSirrolre : perte de charge 01-12-16 à 13:20

g=9.81~\mathrm{m.s^{-2}} / \nu=10^{-6}~\mathrm{m^2.s^{-2}} / \rho=10^3~\mathrm{kg.m^{-3}} / P_{atm}=101300~\mathrm{Pa} / P_{vs}=2340~\mathrm{Pa}
Pour introduire le problème sur lequel je bloque :

Position du problème

1. Conduite d'aspiration
L'eau passe au travers d'une conduite coudée en PVC équipée d'une crépine, pour filtrer l'eau, et d'un clapet anti-retour. Le débit attendu est de 600~\mathrm{m^3.h^{-1}} (cette valeur me permet de connaitre H_{pompe}=18~\mathrm{m} ,\mathcal P_{pompe}=58~\mathrm{kW} et le \mathrm{NPSH=2.2~m} grâce à des courbes de ces grandeurs en fonction du débit)

2. Conduite de refoulement
L'eau passe au travers d'une conduite coudée en acier dont la surface interne est traitée et dont le diamètre ne peut pas excéder \mathrm{2.5~m}


Il s'agit de trouver la section optimale (donc le diamètre) d'un point de vue économique de la conduite de refoulement et de déterminer la pompe à installer

Il nous est précisé que pour calculer l'épaisseur de la conduite on doit se placer environ à mi-hauteur de la conduite de refoulement

Considérations économiques


les coûts sont annuels et calculées pour un mètre linéaire de conduite
-prix de l'acier 1820€/tonne
-prix de pose 900+230D€
-prix de l'énergie 0.06€/kW
-amortissement X pour investissement X_0 sur n années à un taux \tau X=X_0\frac{i(1+i)^n}{(1+i)^n-1}
-prix de l'entretien 0.5% des coûts de construction


Sachant que pour la conduite d'aspiration on est en mesure de calculer toutes les pertes de charges :
\Delta H_{asp}=\Delta H_{crepine}+\Delta H_{clapet}+\Delta H_{coude}+\Delta H_{lineaire}
\Delta H_{asp}=[K_{crepine}+K_{clapet}+\dfrac{\alpha}{\pi}(0.131+1.847(\dfrac{D'}{R})^{\frac{7}{2}})+\lambda\dfrac{L}{D}]\dfrac{v^2}{2g}
où K_{crepine}=3 , K_{clapet}=1.2 , \alpha=\frac{\pi}{2} , D'=\mathrm{300~mm}, R=\mathrm{375~mm} , L=\mathrm{5~m} et \lambda se calcule par le diagramme de Moody avec la rugosité absolue \epsilon=\mathrm{0.1~mm} et le nombre de Reynolds

En revanche c'est sur la conduite de refoulement que je sèche, j'ai la formule de l'épaisseur e en fonction du diamètre D
e=\dfrac{P_{int}D}{2\sigma _a} où on note P_{int} la pression statistique dans la conduite +15% (effets de coups de belier), \sigma _a=235.10^6~\mathrm{N.m^{-2}} la contrainte maximale admissible par l'acier
mais D est inconnu puisque c'est précisément l'iconnu du problème que l'on cherche à determiner donc je ne vois pas comment effectuer ce calcul

Posté par
vanoisere : perte de charge 01-12-16 à 14:57

Bonjour
Je ne suis pas spécialiste de ce type de problème... Je donne tout de même mon avis : l'équation manquante est l'équation "économique". En fonction de toutes les contraintes que tu as étudiées, tu dois pouvoir exprimer le coût annuel en fonction de D puis choisir la valeur de D qui minimise ce coût...

Posté par
iSirrolre : perte de charge 01-12-16 à 14:58

d'accord j'essaye merci

Posté par
iSirrolre : perte de charge 03-12-16 à 16:28

Posons \ell=1~\mathrm{m} pour ramener les sections à des volumes pour un mètre linéaire de conduite.

On a donc le volume une masse d'acier \pi\ell e(D+e)=\pi\ell \dfrac{P_{int}}{2\sigma _a}D^2(1+\dfrac{P_{int}}{2\sigma _a})
les données donne un prix de l'acier 1.82€/kg posons cette valeur \mathbb{P}

donc le prix de l'acier est : \mathbb{P}\rho _a\pi\ell \dfrac{P_{int}}{2\sigma _a}(1+\dfrac{P_{int}}{2\sigma _a})D^2 €

la valeur numérique est donc : 8.08D^2€

avec le prix de pose on a donc une fonction économique en  D qui est :
8.08D^2+230D+900 €

mais je ne sais pas avec quelle courbe la mettre en corrélation

Posté par
vanoisere : perte de charge 05-12-16 à 14:13

Toujours sous réserve...
Plus D est élevé plus les pertes de charges dans la conduite de refoulement sont faibles... Au coût de la pose que tu vient d'exprimer, ne faut-il-il pas ajouter le coût de la pompe (achat, installation et fonctionnement) qui lui va être fonction décroissante de D...

Posté par
iSirrolre : perte de charge 05-12-16 à 14:15

Oui toutes tes remarques sont intéressantes à prendre en compte j'essaye de revoir ca

Posté par
iSirrolre : perte de charge 08-12-16 à 23:40

J'ai recu des éléments de correction, et en effet il fallait prendre en compte:

le coût de construction (acier+pose)
le coût d'amortissement
le coût de fonctionnement (c'est bien ça qui est décroissant avec D comme précédemment évoqué)
le coût d'entretien

Posté par
vanoisere : perte de charge 09-12-16 à 11:56

Très sympa de ta part de me tenir au courant !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !