Inscription / Connexion Nouveau Sujet
Pendule simple
Bonjour,
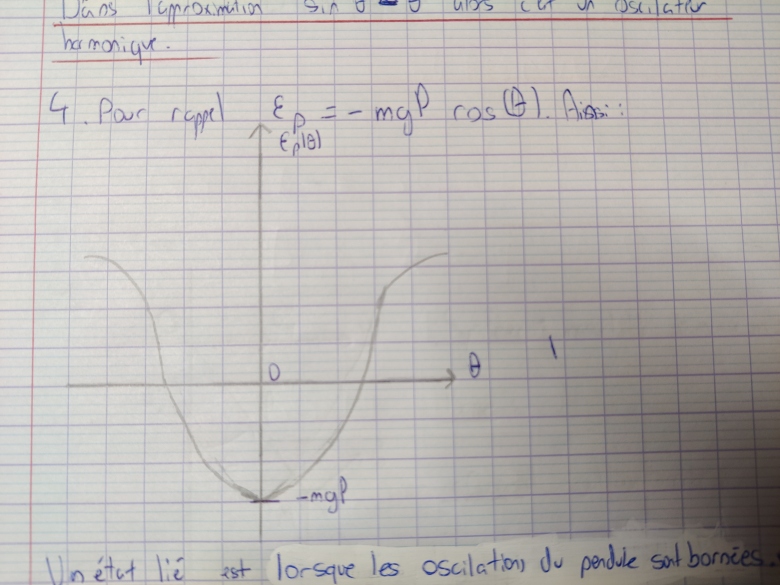
J'ai un dm en mécanique et je bloque sur une question :/. Alors voila, c'est un exercice sur la pendule simple sans frottements. Après un bilan des forces pour trouver l'énergie potentielle, mécanique et l'équation du mouvement, on me demande de tracer le graphe de l'énergie potentielle en fonction de l'angle. J'ai fais ce schéma (au vu de la formule avec un cosinus), on me demande à quelle condition sur la vitesse horizontale initiale on a un état lié ou de diffusion, je vois mal comment faire. J'ai essayé de relier avec la définition je ne vois pas de lien avec la vitesse.
Merci d'avance !
Bonjour
Tu connais la formule :
Em=Ec + Ep
Puisque l'énergie cinétique fait intervenir un carré de vitesse :
Ec
0;
donc :
Em Ep
De plus : l'énergie potentielle, en absence de frottement, est une constante. Dans le repère que tu as utilisé, elle est représentée par une droite horizontale... En tenant compte des inégalités précédentes... Je te laisse réfléchir !
Au max Ep = mgl (au vu de la formule) donc on a Em>mgl quand c'est un état de diffusion. A la fin de mon cheminement j'arrive à v>√2gl(1+cos(teta)) mais ce n'est pas homogène a une vitesse donc il doit y avoir une erreur
En supposant que la vitesse en 
=0 soit Vo ; L'énergie mécanique vaut l'énergie mécanique calculée en =0 :
L'état de diffusion est obtenu lorsque l'énergie mécanique est supérieure à la valeur maximale de Ep : ainsi l'énergie cinétique, donc aussi la vitesse, ne s'annulent jamais.
Je te laisse simplifier. Attention : il faut supposer que la masse m du pendule est reliée à l'axe de rotation par une tige rigide de masse négligeable et non par un simple fil. Dans le cas d'un fil, il faudrait aussi s'assurer que le fil reste constamment tendu...
Annuler
connectez vous