Inscription / Connexion Nouveau Sujet
Pendule simple
Bonjour, je dois faire un compte rendu sur un TP en physique mais je suis un peu perdu à un moment. A une partie du TP, il faut lacher le pendule sans vitesse initiale avec un angle de pi/6, ensuite la meme chose mais en remplacant la masselotte par un aimant et en mettant un autre aimant sous le pendule de telle sorte que les deux aimants s'attirent !
et 3ème manip, la meme chose que la deuxième sauf que cette fois-ci, les aimants de repoussent ! On doit donc tracer les graphiques de ces 3 manip à l'aide d'un logiciel, sur un grand nombre d'oscillations, puisque le but de cette partie est d'étudier l'effet des frottements !
Les questions sont :
1. En negligeant le poids de la lame de métal pour ne conserver que la masse des masselottes ou de l'aimant, établir l'equation fondamentale de la dynamique en supposant que les frottements se comportent comme des frottements fluides : =-

 (.) *vect(e
(.) *vect(e ). On fera l'approximation des petits angles : sin
). On fera l'approximation des petits angles : sin =
= .
.
 =angle initial
=angle initial
2. En faisant l'approximation des petits angles, montrer que  (t) est solution de l'equation differentielle : ml
(t) est solution de l'equation differentielle : ml (..)+
(..)+
 (.)+mg
(.)+mg =0
=0
où m est la masse de la masselotte et l la longueur de la lame.
3. En déduire l'expression théorique de  (t).
(t).
4. Calculer à partir des données expérimentales les périodes d'oscillation du pendule dans les différents cas, en déduire une valeur de  pour chaque cas.
pour chaque cas.
5. Expliquer comment l'on peut calculer  à partir de mesures des amplitudes d'oscillations, et donner cette estimation pour chaque cas.
à partir de mesures des amplitudes d'oscillations, et donner cette estimation pour chaque cas.
J'ai trouvé avant  =0.0213, c'est le facteur de conversion entre volts et rad/s du tachymètre.
=0.0213, c'est le facteur de conversion entre volts et rad/s du tachymètre.
 (.)(t) est la vitesse angulaire, c'est la dérivée de
(.)(t) est la vitesse angulaire, c'est la dérivée de  (t) / dt
(t) / dt
(.) et (..) sont la dérivée et la dérivée seconde de  (t).
(t).
Voilà, j'espere que vous pourrez me mettre sur la voie, merci beaucoup.
Bonsoir,
Pour obtenir l'équation différentielle vérifiée par  , il faut appliquer à la masse ponctuelle la relation fondamentale de la dynamique et la projeter sur u
, il faut appliquer à la masse ponctuelle la relation fondamentale de la dynamique et la projeter sur u .
.
J'imagine que la lame se comporte comme un fil sans raideur , ce qui permet d'assimiler le pendule à un pendule simple. En notant T la force exercée par la lame sur la masse, on obtient :
En coordonnées polaires, pour un mouvement circulaire, l'expression de l'accélération est :
En projetant sur u :
:
pour les faibles amplitudes, cela se simplifie :
En posant :
cela donne :
La suite est un grand classique : tu obtient un mouvement sinusoïdal amorti dont je te laisse démontrer l'équation. Cela devrait ressembler à :
où A et  sont deux constantes dépendant des conditions initiales. L'étude de la diminution exponentielle de l'amplitude au cours du temps doit permettre une mesure de
sont deux constantes dépendant des conditions initiales. L'étude de la diminution exponentielle de l'amplitude au cours du temps doit permettre une mesure de  donc ensuite de
donc ensuite de  .
.
Cela devrait déjà pas mal t'aider, sous réserve, encore une fois, que la lame ne présente pas de raideur...
J'ai trouvé avant
 =0.0213, c'est le facteur de conversion entre volts et rad/s du tachymètre.
=0.0213, c'est le facteur de conversion entre volts et rad/s du tachymètre. J'allais oublié : il semble bien que
 désigne dans ce problème, deux grandeurs différentes :
désigne dans ce problème, deux grandeurs différentes :
1° : le coefficient de frottement : c'est ce "
 "- là que j'ai utilisé dans mon message précédent.
"- là que j'ai utilisé dans mon message précédent.
2° : la constante de ton tachymètre. Attribue à cette constante un autre symbole (k ou
 ou....) . Une même lettre ne peut pas représenter deux grandeurs différentes dans un même problème !
ou....) . Une même lettre ne peut pas représenter deux grandeurs différentes dans un même problème !Merci mais je ne comprends pas certaine choses, vous faites la premiere question ? Si oui, je ne comprends pas pourquoi vous dites que +
+
= m.
puisque c'est ce que l'on veut montrer non ?
Et qu'est ce que vect(u ) et vect(ur) pour vous ?
) et vect(ur) pour vous ?
Bonsoir
je ne comprends pas pourquoi vous dites que
Tu voudrais "démontrer" la relation fondamentale de la dynamique ??? Les lois sur la dynamique de Newton ne se démontrent pas ! Elles se justifient pas l'ensemble de leurs conséquences : mouvement des planètes... etc...
La question est mal posée ; il s'agit en fait de faire l'inventaire des forces appliquées à la masse m, ce qui permet d'écrire l'équation précédente.
Et qu'est ce que vect(u) et vect(ur) pour vous ?
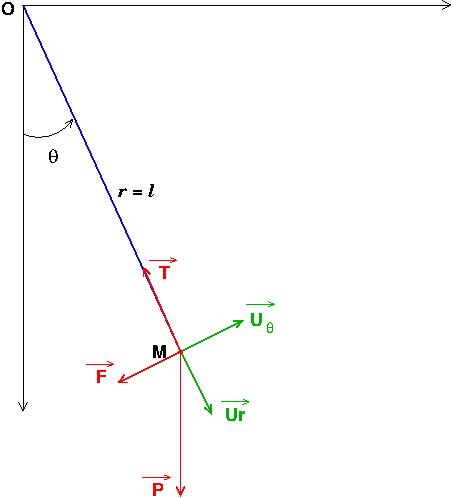
Si tu appelles O le point fixe et M la masse ponctuelle, tu obtiens un schéma du type ci-dessous. Le vecteur ur est un vecteur unitaire colinéaire au vecteur OM. Le vecteur u
 est un vecteur unitaire ayant le sens et la direction du vecteur vitesse. La figure correspond donc à un instant où le pendule se déplace vers la droite. Le plan de figure est le plan vertical auquel appartient la trajectoire du M.
est un vecteur unitaire ayant le sens et la direction du vecteur vitesse. La figure correspond donc à un instant où le pendule se déplace vers la droite. Le plan de figure est le plan vertical auquel appartient la trajectoire du M.
Le pendule simple est un grand classique des cours de dynamique. Tu l'as sûrement étudié en cours...
J'ai réussi les questions 1 et 2 mais je voudrais votre avis pour la 3
en remplaçant puis en isolant  (t), je trouve:
(t), je trouve:
 (t)=(ml
(t)=(ml (t)(..)+
(t)(..)+
 (t)(.))/ -mg
(t)(.))/ -mg
Merci d'avance
Bonsoir
Je t'ai fourni la démonstration dans mon premier message :
Essaie de comprendre la démonstration qui va avec mais, de toutes façons, la résolution d'une équation différentielle du second ordre est un grand classique du cours !
Mais je ne comprends pas car quand on veut résoudre une équation différentielle du second ordre, on trouve l'équation caractéristique, on calcule delta et on etudie son signe non ?
Mais je ne comprends pas car quand on veut résoudre une équation différentielle du second ordre, on trouve l'équation caractéristique, on calcule delta et on etudie son signe non ?
Absolument ! Mais cela : je ne l'ai pas écrit : c'est de l'application directe du cours que tu peux sûrement faire sans aide. Je t'ai juste indiqué le résultat final pour le régime pseudo périodique qui correspond à
 <
< o
o


