Niveau licence

Pendule pesant

Posté par
Pikimidb 14-12-17 à 21:54

Bonsoir,

Je prépare un TP et je ne suis pas sûr de toutes mes réponses, voici le contexte :

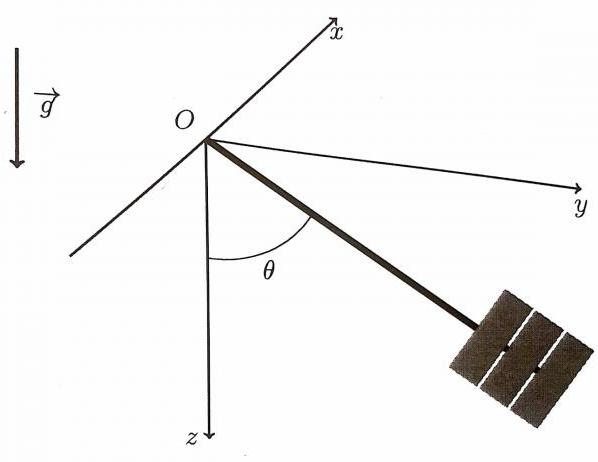
n cylindres homogènes identiques sont attachés au bout d'une tige rigide de masse m_t et de longueur l (voir schéma).
Les cylindres ont une hauteur h, un rayon r et une masse m_c.
L'ensemble est assimilé à un solide indéformable S appelé pendule pesant.
Le mouvement du pendule autour du point d'attache O est décrit par l'angle et obéit à l'équation du mouvement qui suit :
$I_{Ox} \ddot{\theta}+MgOCsin\theta = 0$ (1)
avec M = m_t+nm_c, I_Ox le moment d'inertie du pendule par rapporte à son axe de rotation (Ox) et C le centre de masse du pendule (on fera l'approximation OC l).
On fait alors différentes approximations sur le pendule :

1) pendule idéal : I_Ox nm_cl²

2) pendule réaliste : I_Ox $\frac{1}{3}m_tl^2+\frac{1}{4}nm_c(r^2+\frac{n^2h^2}{3})+nm_cl^2$

dans l'approximation des petits angles, on a alors l'équation du mouvement du pendule idéal :

$\ddot{\theta }+w_0^2\theta =0$
avec :
$w_0 =( \frac{Mgl}{I_{Ox}})^\frac{1}{2}$

a) Dans le cas du pendule idéal, la pulsation w₀ dépend-elle de la masse du pendule ? Dépend-elle de l'angle de déviation maximale ₀ ?
Dans le cas réaliste, exprimer le rapport des masses de la tige et d'un cylindre m_t/m_c en fonction de w₀ et des paramètres de l'expérience.

Dans le cas du pendule idéal, j'ai mis que :

$w_0 =( \frac{Mgl}{I_{Ox}})^\frac{1}{2}\Leftrightarrow w_0 = (\frac{g}{l})^\frac{1}{2}+(\frac{m_t}{nm_cl^2})^\frac{1}{2}$

donc, la pulsation ne dépend pas de la masse du pendule.
Pour ₀, je ne sais pas, je pense que oui (le terme de droite dans mon égalité) mais je ne sais pas comment le démontrer.

Dans le cas réaliste, j'ai trouvé que :

m_t/m_c = $\frac{\frac{ngl}{w_0}-\frac{1}{4}n(r^2+\frac{n^2h^2}{3})-nl^2}{\frac{1}{3}l^2-\frac{gl}{w_0}}$ .

b) De manière générale en dehors de l'approximation des petits angles, l'équation du mouvement a une solution correspondant à des oscillations anharmoniques dont ni la loi horaire, ni la pulsation ne peuvent être calculées analytiquement.
Une solution approchée peut-être obtenue par un développement limité du terme en sin de l'équation (1), la période est alors donnée par :

T = $T_0[1+\frac{1}{4}sin^2(\frac{\theta _0}{2})+\frac{9}{64}sin^4(\frac{\theta _0}{2})+...]$
avec T₀ = 2/w₀
Montrer qu'aux petits angles, on retrouve la période d'un oscillateur harmonique.

Je ne sais pas comment procéder pour cette question, faut-il faire l'approximation sin = , puis dire que le terme en 1 est très supérieur à toute la somme?

Il y a ensuite une question avec un développement limité, mais ça c'est bon.

Merci d'avance pour l'aide apportée !

Pendule pesant

Posté par re : Pendule pesant 14-12-17 à 22:22

Bonsoir
Tu te débrouilles bien dans l'ensemble. Juste deux compléments.
1° : Dans le cas des oscillations de très faible amplitude, l'équation différentielle du mouvement : $\ddot{\theta }+w_0^2\theta =0$ admet une solution différentielle de la forme :

$\theta=\theta_{0}\cdot\cos\left(\omega_{0}.t+\varphi\right)$
où _o est l'amplitude et une constante dépendant des conditions initiales. On voit bien que la période vaut :

$T_{0}=\frac{2\pi}{\omega_{0}}$
et ne dépend pas de l'amplitude.
2°) Il faut bien comprendre que la formule du développement limité :

$T = T_0[1+\frac{1}{4}sin^2(\frac{\theta _0}{2})+\frac{9}{64}sin^4(\frac{\theta _0}{2})+...]$
n'a de sens que pour des angles faibles. dans ces conditions :

$1\gg\frac{1}{4}sin^{2}(\frac{\theta_{0}}{2})\gg\frac{9}{64}sin^{4}(\frac{\theta_{0}}{2})\gg...$
Pour les très faibles amplitudes, les termes en sinus sont négligeables devant 1 : TT_o