Bonjour
Pour déterminer sans ambiguïté l'équation horaire, il faut connaître les conditions initiales : abscisse et vitesse à l'instant date t=0.

2) En répondant à la question 2, tu devrais trouver :  

  
(Xo étant l'abscisse du centre d'inertie de la masse à l'instant t = 0 où il est laché sans vitesse initiale)

Et c'est alors facile de répondre aux autres questions.


... Et donc commence par essayer de trouver la réponse ci-dessus.

Sauf distraction.  

Bien évidemment ...

La plupart des énoncés sont plein de lacunes.
Si on ne suppose pas une volée de "non dits" alors on est bloqué.

L'enseignement n'est plus ce qu'il était, les énoncés sont souvent incomplets et  même très souvent remplis d'idioties, il faut bien faire avec.

Ici, l'énoncé suit la règle quasi générale ... il y manque plein de choses.

On peut donc , soit :
a) demander les conditions initiales ...
Question qui recevra certainement la réponse "Je ne sais pas, j'ai copié l'énoncé au complet".

b) Supposer les conditions initiales les plus plausibles ... et les indiquer.
Quitte au questionneur de les modifier si c'est lui qui les a supprimées de l'énoncé initial ... ce qui n'est probablement pas le cas.

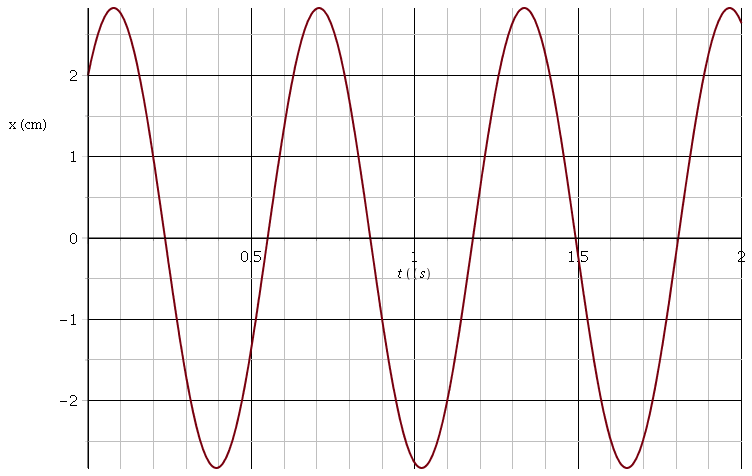
bjr je m'excuse j'avais oublier un paragraphe de l'énonce en fait le voici: la solution géneral de l'équation différentielle du mouvement s'écrit sous la forme: x(t)=xmcos(2π/To+&o) Xm est l'amplitude du mouvement, To la période et &o est la phase à l'origine .on écarte le solide de sa position d'équilibre d'une distance X telle que X=+2,0cm puis on le lance avec une vitesse de composante Vxo=0,20m/s.  c'est la suite de  de l'exercice sur le pendule élastique MERCI

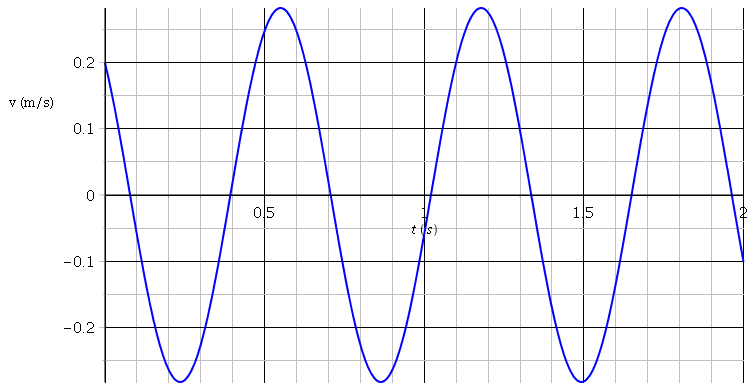
OK. Dans ces conditions, commence par exprimer v(t) en dérivant par rapport à t l'expression de x(t)fournie par l'énoncé.
Etudie ensuite les deux cas particuliers :
x(0)=2,0.10^-2m
v(0)=0,20m/s
Cela va te conduire à un système de deux équations à deux inconnues : l'amplitude X_m et la phase initiale .

ok merci j'ai trouver ces deux valeurs Xm=0,0282m et tang&=-1 donc &=-π/4

je ne sais comment faire pour déterminer les différents temps t1 et t2

D'accord avec toi !

pourrai je remplacer ces différentes valeurs sur la solution général de l'équation différentielle pour déterminer les différents temps demander??

Maintenant, tu connais exactement l'expression de x(t) et celle de v(t). Il faut raisonner à partir de ces deux expressions pour répondre aux questions posées. Pour t'aider un peu et même te permettre de "t'auto corriger", voici les courbes correspondant à x(t) en rouge et à v(t) en bleu.