Inscription / Connexion Nouveau Sujet
Pendule de torsion
philou28
Bonjour
Je cherche l'équation différentielle du pendule de torsion suivant :
Le pendule de torsion est constitué d'une tige de masse m et de longueur L avec deux masses M sphérique de rayon R, situées à une distance d du milieu O de la tige.
On modélise les actions mécaniques exercées par le fill de torsion sur la tige par :
Une résultante R vecteur
Un moment en O correspondant à un couple de rappel élastique :
lors d'une torsion d'un angle 
du fill autour de Oz
L'expression du moment est :
Mo=-
uz
JOz est le moment d'inertie du pendule par rapport à l'axe Oz
D'aprés le tMC scalaire :
JOzd
/dt = -
Est ce bon ?
Merci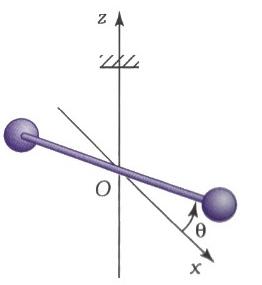
***Image recadrée***
Bonsoir
Est ce bon ?
Oui ! comme
est la dérivée par rapport au temps de , tu obtiens en fait une équation différentielle du second ordre :
Dont la solution est sinusoïdale de période :
Si la détermination du moment d'inertie en fonction des masses et de la géométrie du pendule est simple, la mesure de la période des oscillations permet de déterminer .
Sinon, il y a aussi des méthodes statiques : voir par exemple ce TP :
J'avais vu ce tp sur internet mais je ne vois pas comment l'utiliser avec mon pendule de torsion...
Comment en mesurant la période je peut déterminer en utilisant la formule T=2pi
J/ ?
Je crois avoir trouvé :
Je mesure une première période T1
Ensuite une deuxième T2 en ajoutant deux même masses m de chaque coté, ce qui fait un nouveau moment d'inertie J'Oz=JOz+2md² puisque que chaque masse est distantes de d du centre O
En effectuant T1/T2 je détermine JOz et ensuite avec l'une des période je détermine .
On aura une meilleur précision des périodes si les oscillations sont grandes je pense.
cela fonctionne ?
Merci
si les conditions initiales sont ;
(0)=0 et d/dt='
la solution de l'équation énoncée plus haut est :
(t)='/0sin(0t)
est ce bon ?
Bonsoir,
Si tu notes :
m : masse de la tige homogène de longueur totale L,
M : masse d'une des deux boules de rayon R, chaque boule étant supposée homogène,
d : distance entre l'axe de rotation matérialisé par le fil et le centre d'une boule, les deux boules étant placées symétriquement par rapport à cet axe, l'application du théorème de Huyghens conduit à l'expression du moment d'inertie par rapport à l'axe de rotation :
Connaissant ainsi le moment d'inertie, une mesure précise de la période permet la détermination de la constante de torsion du fil.
On aura une meilleur précision des périodes si les oscillations sont grandes je pense.
Attention : la période est la même quelle que soit l'amplitude angulaire des oscillations. Pour améliorer la précision de la mesure sur T, tu mesures la durée correspondant, par exemple, à 10 périodes.
Bonsoir
Merci pour la précision sur Joz
J'ai résolu l'équation plus haut, est elle bonne ?
Maintenant sur l'exercice on me dit que l'on tient compte d'une force de frottement :
f=-fv
Quel est le moment par rapport à oz de cette force de frottement pour que je l'incorpore dans l'équation ?
merci
J'ai résolu l'équation plus haut, est elle bonne ?
Quelle équation ?
Maintenant sur l'exercice on me dit que l'on tient compte d'une force de frottement :
f=-fv
Force appliquée de quelle façon ? Dans un tel problème, il faut donner des indications permettant d'obtenir le moment de cette force par rapport à l'axe de rotation. De plus, une telle force risque de modifier la direction de l'axe matérialisé par le fil qui risque de ne pas rester vertical... Es-tu sûr qu'il ne s'agit pas plutôt d'un couple de frottement ?
l'équation : J0zd/dt +=0
si les conditions initiales sont ;
(0)=0 et d/dt=' le ' est un point
la solution est :
(t)='/0sin(0t)
Voila ce que dit l'exercice :
Du fait de la présence d'un frottement du au déplacement des masses dans l'air, un amortissement des oscillations à lieu. On modélise les forces de frottements par
F=-fv (en vecteurs) appliquée au centre de chacune des masses,
v désignant leur vitesse et f le coef.
Établir la nouvelle équation différentielle en et indiquer la nature de la solution, sachant que l'amortissement est très faible.
Merci beaucoup pour vos aides...
En fait on me dit que Joz est le le moment d'inertie du pendule par rapport l'a l'axe Oz. et l'énoncé précise de ne pas chercher à l'exprimer.
Il faut trouver les équation sans chercher à l'exprimer donc on garde Joz dans toutes les équations je pense.
la vitesse v de chaque centre de boule est v = d.'
La force de frottement exercée sur une boule vaut : F=f.v = f.d.'
Le moment de chaque force par rapport à l'axe de rotation est MF=-F.d = -f.d2.'
Ton équation différentielle du mouvement devient :
Sachant que l'amortissement est très faible, tu vas obtenir un mouvement pseudo-périodique.
d' veut dire dérive première de ?
et d²' veut dire dérivée seconde de ?
la solution est bonne pour l'équation sans frottement?
merci
J'ai déjà défini d comme la distance entre l'axe de rotation et le centre d'une boule... Tu as bien étudié en cours la notion de moment de force par rapport à un axe ?
Oui j'ai bien compris ce que tu as écrit c'est juste sur la compréhension sur l"écriture de ' du post où il y a l'équation
Ensuite on réalise l'expérience de Cavendish en approchant deux masses M' et on calcul G en mesurant c : angle de déviation au repos avec l'influence des masse et sans les masses
Je pense avoir trouver G
Mais comment mesurer expérimentalement cet angle c
Mais comment mesurer expérimentalement cet angle
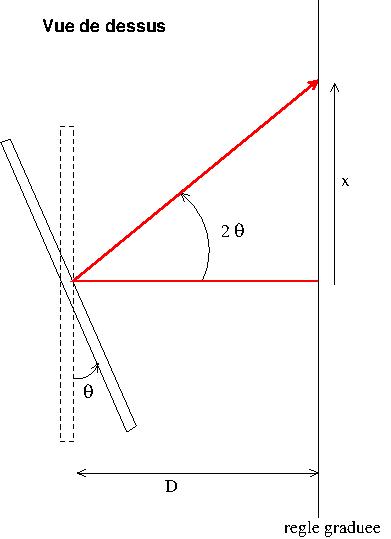
La méthode dite de "Poggendorff" est relativement simple et précise (voir schéma d'une vue de dessus)et ne perturbe pas la position d'équilibre. On fixe à la tige horizontale en rotation un petit miroir plan dont le centre est sur l'axe de rotation. On éclaire celui-ci avec un faisceau de lumière parallèle horizontal de faible diamètre (faisceau laser par exemple) de sorte que le faisceau se réfléchisse sur lui-même pour
=0.
lorsque le pendule de torsion tourne d'un angle
non nul, le faisceau lumineux réfléchi tourne d'un angle 2 (voir lois de Descartes) que l'on peut déterminer en mesurant la déviation x du spot lumineux sur une règle graduée.
x = D.tan(2
). Bien sûr, dans la réalité, les angles sont beaucoup plus faibles que sur mon schéma.
Avec la force de frottement en considération, est ce que cela remet en cause la détermination du coef calculer sans frottement ?
Avec la force de frottement en considération, est ce que cela remet en cause la détermination du coef calculer sans frottement ?
Bien sûr que non !
La constante de raideur
du fil, dépend de la longueur du fil métallique, de son diamètre et de la nature du métal. Si aucun de ses trois paramètres n'est modifié au cours de l'expérience, on peut considérer comme une constante.
Annuler
connectez vous