Inscription / Connexion Nouveau Sujet
pendule
Bonsoir,
J'ai un exercice sur le pendule simple:
1) Déterminer l'énergie mécanique du pendule.
Pour l'énergie cinétique Ec: Ec=mv²/2
Exprimons v² en coordonnée polaire: OM=r er ;dOM/dt=r(d /dt) e
/dt) e
Ainsi Ec=I(d /dt)²/2 avec I=mr²
/dt)²/2 avec I=mr²
Pour l'énergie potentielle U: F=- U(r)/
U(r)/ r ; donc U=-
r ; donc U=- F.dr=-mg(r2-r1) avec r2-r1=r. Et là je doute, U=Ux+Uy, Ux=0 donc U=Uy=-mgrcos
F.dr=-mg(r2-r1) avec r2-r1=r. Et là je doute, U=Ux+Uy, Ux=0 donc U=Uy=-mgrcos .
.
E=Ec+U
2)Déterminer l'équation du mouvement.
Je sais pas trop quoi dire.
3)Déterminer  (t) quand:
(t) quand:
a) (0)=
(0)= 0 et d
0 et d /dt=0
/dt=0
E se conserve donc sa dérivée temporelle est nulle.
dE/dt=I(d /dt)(d²
/dt)(d² /dt²) + mgrsin(
/dt²) + mgrsin( )(d
)(d /dt)=0.
/dt)=0.
On factorise par d /dt donc soit d
/dt donc soit d /dt=0 soit I(d²
/dt=0 soit I(d² /dt²)+mgrsin(
/dt²)+mgrsin( )=0
)=0
Le cas d /dt ne nous intéresse pas car cela voudrait dire que le pendule est immobile.
/dt ne nous intéresse pas car cela voudrait dire que le pendule est immobile.
Les oscillations sont petites alors on peut approximer sin( ) par un développement limité d'ordre 2: sin(
) par un développement limité d'ordre 2: sin( )
)
 .
.
Résolvons l'équation différentielle obtenue: (d² /dt²)+mga/I
/dt²)+mga/I  =0
=0
 (t)=C1cos(wt)+C2sin(wt).
(t)=C1cos(wt)+C2sin(wt).
Déterminons C1 et C2:
theta (0)=C1= 0
0
d /dt (0)=wC2=0 donc C2=0
/dt (0)=wC2=0 donc C2=0
 (t)=
(t)= 0cos(wt)
0cos(wt)
Que représente w ? C'est (mga/I)1/2 ?
b)quand  (0)=
(0)= 0 et d
0 et d /dt (0)=w
/dt (0)=w
 (0)=C1=
(0)=C1= 0
0
d /dt (0)=wC2=w donc C2=1
/dt (0)=wC2=w donc C2=1
 (t)=
(t)= 0cos(wt)+sin(wt)
0cos(wt)+sin(wt)
Démontrer que la période des oscillations du pendule est P=2 /w0 (1+1/16
/w0 (1+1/16  ²max +11/3072
²max +11/3072  4max+...) avec w0 = (mgr/I)1/2 et
4max+...) avec w0 = (mgr/I)1/2 et  max est un angle pour lequel l'énergie cinétique est nulle. Estimer le domaine d'applicabilité de cette équation.
max est un angle pour lequel l'énergie cinétique est nulle. Estimer le domaine d'applicabilité de cette équation.
Je sais pas trop quoi dire, on utilise généralement la formule P=2 /w0 pour déterminer la période.
/w0 pour déterminer la période.
PS: Comment faire des fractions et mettre un/deux point(s) sur le  ?
?
Bonsoir
Pour l'équation du mouvement, la méthode la plus logique compte tenu de la question précédente consiste à écrire que l'énergie mécanique est constante. Sa dérivée par rapport au temps est nulle à chaque instant.
Tu as fait la démonstration à laquelle je pensais ensuite... Je pense que la question 2 est imprécise. Il s'agit d'établir l'équation différentielle dont  est solution.
est solution.
L'équation différentielle obtenue est de la forme :
 '' + w2.
'' + w2. =0. Par identification...
=0. Par identification...
Pour les deux points de la dérivée seconde, il faut utiliser l'éditeur d'équations Tex disponible dans le menu grâce à l'icône LTX.
La dernière question concerne une expression approchée de la période lorsque l'amplitude  max (ou
max (ou  o ; les deux notations sont utilisées dans ton énoncé...) est trop grande pour qu'il soit possible de poser avec une précision suffisante :
o ; les deux notations sont utilisées dans ton énoncé...) est trop grande pour qu'il soit possible de poser avec une précision suffisante :
sin( )
)
 et cos(
et cos( )
) 1-
1- 2/2
2/2
Le mouvement est toujours périodique mais il n'est plus sinusoïdal.
L'énoncé ne semble proposer aucune piste pour établir l'expression de la période pour les grandes amplitudes. Une des méthodes possibles consiste à établir l'expression exacte de la période sous forme d'une intégrale déduite de la conservation de l'énergie mécanique ou du théorème de l'énergie cinétique. Un développement limité conduit alors à l'expression demandée.
J'ai eu l'occasion de faire la démonstration sur ce document à partir de la page 10 :
![]()
Attention : le reste du document concerne les balanciers de précision utilisés en horlogerie : pas vraiment ta préoccupation immédiate !
Pour l'energie potentielle U: je pense mettre en fait U= (Ux2+Uy2)1/2 or Uy=0 donc U=Ux.
Pour w dans la résolution de l'équation différentielle, je pense pas que ce soit (mgr/I)1/2 car après ils disent w0=(mgr/I)1/2.
Donc pour la 2) je met juste  " +w2 sin(
" +w2 sin( )=0 ?
)=0 ?
J'ai aussi comme autre question l'équation du mouvement pour des petites oscillations sans frottement, et avec frottement.
Et pour le facteur (1+1/16...) pour la période, comme ce n'est pas le DL de sin( ) je vois pas ce que c'est.
) je vois pas ce que c'est.
Concernant les notations :
Il est assez habituel de noter  o la pulsation propre c'est à dire la pulsation des oscillations libres. La lettre
o la pulsation propre c'est à dire la pulsation des oscillations libres. La lettre  étant alors utilisée pour désigner la pulsation en régime sinusoïdal forcé. Tu as sûrement vue cela lors de l'étude des circuits électriques.
étant alors utilisée pour désigner la pulsation en régime sinusoïdal forcé. Tu as sûrement vue cela lors de l'étude des circuits électriques.
Si dans ce problème, il n'y a pas vers la fin une étude de régime sinusoïdal forcé, il n'y a pas d'inconvénient à noter indifféremment  ou
ou  o. Fais comme le demande l'énoncé.
o. Fais comme le demande l'énoncé.
Il s'agit du développement limité de :
que j'ai effectué au milieu de la page 13 mais il faut le pousser à l'ordre supérieur si tu veux obtenir comme demandé un terme en  max4
max4
Il existe une autre démonstration utilisant l'analyse de Fourier mais cela m'étonnerait qu'il s'agisse de celle attendue ici dans la mesure où toutes les questions précédentes utilisent la conservation de l'énergie mécanique.
Rectification :
Il faut effectuer un développement limité de :
remplacer par
comme je l'ai fait dans mon document conduit bien au terme correct en
mais n'est pas assez rigoureux pour obtenir une estimation correcte du terme en
;
Le reste de l'exercice est assez simple mais il y a pour cette dernière question une brutale discontinuité de niveau !
J'ai oublié un détail qui a son importance à la fin des questions...
"Utiliser la série de Taylor pour l'intégrale elliptique complète de première espèce K(k)= /2(1+k²/4 +9k4/64 +...) (k<1)
/2(1+k²/4 +9k4/64 +...) (k<1)
Je me suis aidé du document, même si parfois on avait pas la même notation.
Prenons le cas particulier  max : Ec=0 donc E=-mgrcos
max : Ec=0 donc E=-mgrcos max. Ainsi, I
max. Ainsi, I²/2 -mgrcos
 =-mgrcos
=-mgrcos max
max
²=2mgr/I (cos
 -cos
-cos max)
max)
Prenons un quart de période se déplacant dans le sens positif.

 max0 d
max0 d /(cos
/(cos -cos
-cos max)1/2=
max)1/2= P/40
P/40  2 w0 dt=
2 w0 dt= 2 w0P/4
2 w0P/4
P=2 2 /w0
2 /w0 
 max0 d
max0 d /(cos
/(cos -cos
-cos max)1/2
max)1/2
Et là, je sais pas trop quoi faire
C'est vrai que j'utilise la notation  au lieu de
au lieu de  mais cela ne devrait pas vraiment te gêner à ton niveau ! Reprend mon document page 13 : il te faut passer à l'angle moitié pour aboutir à l'expression :
mais cela ne devrait pas vraiment te gêner à ton niveau ! Reprend mon document page 13 : il te faut passer à l'angle moitié pour aboutir à l'expression :
avec :
Développement limité :
Petite indication d'ordre mathématique pour te faire gagner du temps :
Bon courage pour la suite !
L'énoncé fait intervenir le moment d'inertie du pendule par rapport à l'axe de rotation. On peut donc supposer qu'il s'agit d'un pendule composé et non d'un pendule simple, ce qui autorise des amplitudes  m proches de 180° par valeurs inférieures. La position
m proches de 180° par valeurs inférieures. La position  =180° est une position d'équilibre instable.
=180° est une position d'équilibre instable.
Pour t'aider à conclure sur les domaines de validité des différentes formules approchées :
T=To ;
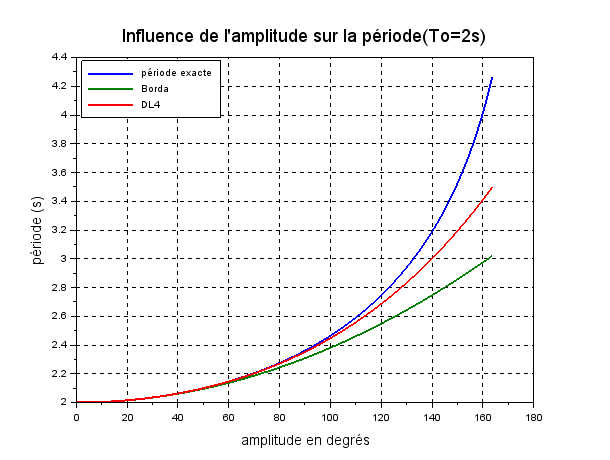
j'ai représenté les variations en fonction de l'amplitude de :
* la période exacte déduite du calcul intégral direct (les logiciels scientifiques et les calculatrices modernes font cela avec une très bonne précision) (courbe bleue)
* la période déduite de la formule de Borda (terme en  m2 seulement pris en compte) (en vert)
m2 seulement pris en compte) (en vert)
* la période déduite de la formule de ton énoncé (en rouge).
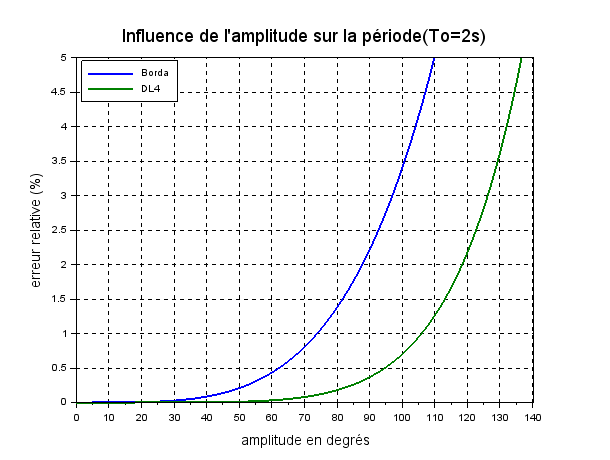
Tu peux déjà en déduire un certain nombre de renseignements. Pour t'aider à mieux quantifier les choses, j'ai représenté en dessous les erreurs relatives introduites par les deux méthodes.
Avec tout cela, tu devrais être capable de terminer...
Je ne sais pas si ma méthode pour déterminer l'énergie potentielle est correcte, je trouve U=-mgl mais je rajoute cos( ) car la projection du poids est uniquement verticale. Est-ce une méthode valable et en existe t'il d'autre ?
) car la projection du poids est uniquement verticale. Est-ce une méthode valable et en existe t'il d'autre ?
De plus, dans le document il y a marqué que l'énergie potentielle est mgl(1-cos ).
).
Pour ma formule générale de résolution de l'équation différentielle, je pense mettre C1cos(w0t)+C2sin(w0t) à la place de w, comme on utilise pas w.
Dans le document, "Cette équation admet une solution sinusoidale de la forme:  =
= max cos(w0 t -
max cos(w0 t - )"
)"
S'agit t'il d'une solution générale identique à la mienne avec C1cos... ou bien une différente ? Et, je ne comprends pas comment on arrive à T0 =2 /w0 avec ça.
/w0 avec ça.
Tu sais depuis longtemps que l'énergie potentielle de pesanteur peut s'écrire Ep=m.g.z où z est l'altitude du centre de gravité G par rapport à un niveau d'altitude nulle arbitrairement choisi.
Ton corrigé semble prendre le niveau d'altitude nulle correspondant à la position de G à l'équilibre stable soit pour  =0.
=0.
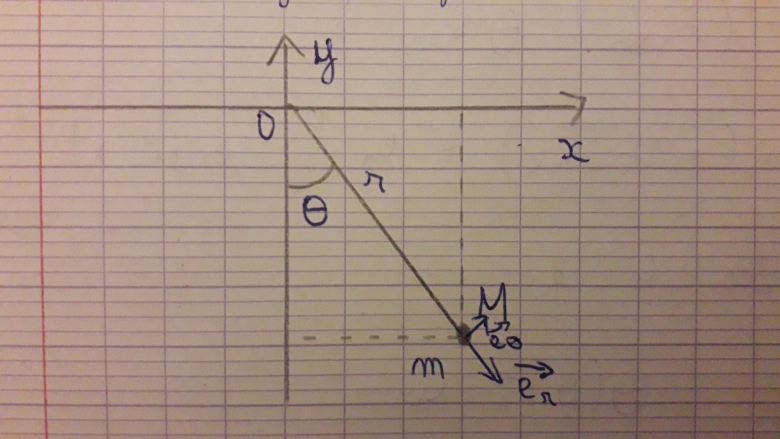
Ton schéma note "r" la distance de G à l'axe de rotation. Complète ton schéma pour faire apparaître l'altitude z pour une position quelconque du pendule. Tu vas pouvoir montrer facilement :
z=r.[1-cos( )]
)]
Toute équation différentielle du second ordre de la forme :
f"(t)+ o2.f(t)=0
o2.f(t)=0
admet une solution générale de la forme :
f(t)=C1.cos( o.t)+C2.sin(
o.t)+C2.sin( o.t)=A.cos(
o.t)=A.cos( o.t-
o.t- ).
).
Tu peux développer cos( o.t-
o.t- ) pour t'en convaincre...
) pour t'en convaincre...
La période est la plus petite augmentation de t qui conduit à une même position et une même vitesse, c'est donc la période de la fonction cosinus :  o.T=2
o.T=2
Il s'agit là des bases... à mille lieues de la dernière question sur l'influence de l'amplitude sur la période... Juste par curiosité : c'est ton professeur qui ta fourni cet exercice où tu l'as trouvé sur un livre ?
D'accord, je viens de comprendre pour l'énergie potentielle, en mettant Ep=0 à  =0 je trouve aussi mgr(1-cos
=0 je trouve aussi mgr(1-cos ), et en mettant Ep=0 à
), et en mettant Ep=0 à  =
= /2 je trouve -mgrcos
/2 je trouve -mgrcos . Dans l'énoncé, je pense que Ep=0 à
. Dans l'énoncé, je pense que Ep=0 à  /2.
/2.
En développant, grâce à la formule cos(a-b)=cosacosb+sinasinb je trouve C1=Acos et C2=Asin
et C2=Asin , c'est bien ça ?
, c'est bien ça ?
Oui, c'est un devoir maison.
Un ami m'a montré pour la question sur la période et c'est bon j'ai trouvé le bon résultat.
Juste, je ne comprends pas la différence entre P et P0, P0=2 /w0 et P=2
/w0 et P=2 /w0 facteur de tout le reste dans un cas général et en approximant sin
/w0 facteur de tout le reste dans un cas général et en approximant sin par
par  dans l'équation du mouvement P=P0?
dans l'équation du mouvement P=P0?
Pour la dernière question, je sais pas trop quoi répondre pour l'équation du mouvement avec frottement.
J'ai pas beaucoup fait de mécanique et je sais plus comment exprimer la force de frottement, j'appelle force de frottement f, l'équation du mouvement devient d2 /dt2 + (mg+f)r/I sin
/dt2 + (mg+f)r/I sin =0 ? Et comment note t'on la force de frottement ?
=0 ? Et comment note t'on la force de frottement ?
Tu progresses ! OK pour les identifications.
Tu peux choisir le niveau d'altitude nulle de façon totalement arbitraire. Les différents choix possibles ne diffèrent que par une constante. Puisque l'équation différentielle du mouvement s'obtient en dérivant par rapport au temps la relation de conservation de l'énergie mécanique, on obtient la même équation dans tous les cas puisque la dérivée par rapport au temps d'une constante est nulle.
Po désigne la période dans le cas des mouvements de très faibles amplitudes, lorsqu'il est , comme tu l'as écrit, possible de poser sin( )
)
 avec une bonne précision. Graphiquement, on voit bien que la courbe représentant la période réelle (courbe bleue) est quasiment confondue avec sa tangente horizontale pour une amplitude inférieure à une douzaine de degrés mais bien sûr : tout dépend de la précision souhaitée.
avec une bonne précision. Graphiquement, on voit bien que la courbe représentant la période réelle (courbe bleue) est quasiment confondue avec sa tangente horizontale pour une amplitude inférieure à une douzaine de degrés mais bien sûr : tout dépend de la précision souhaitée.
Tu n'as pas postée d'énoncé précis sur la modélisation des frottements. Très souvent, pour les très faibles vitesses comme ici, on modélise l'action de l'air comme une force de frottement proportionnelle à la vitesse ; cela pourrait conduire à une équation différentielle de la forme suivante :
Soit, pour les oscillations de faible amplitude :
A vérifier par rapport à l'énoncé et à adapter en fonction des notations...
Dans mon énoncé, il y a juste marqué "Déterminer l'équation du mouvement du pendule simple avec frottement."
Je ne sais pas comment exprimer le frottement. Si on modélise le frottement comme proportionelle à la vitesse, on devrait trouver E=I(d /dt)2f/2 -Mgacos
/dt)2f/2 -Mgacos mais on peut pas dire que la dérivée par rapport au temps est nulle comme la l'énergie mécanique n'est plus conservative ?
mais on peut pas dire que la dérivée par rapport au temps est nulle comme la l'énergie mécanique n'est plus conservative ?
Je pense qu'il s'agit de faire intervenir une action de frottement proportionnelle à la vitesse. On pourrait aussi imaginer un frottement de type solide au niveau de l'axe de rotation :cela se modéliserait par un couple dont la valeur absolue serait fixe mais dont le signe serait celui de . Pas très évident à traiter car on obtient deux équations différentielles différentes à résoudre selon le signe de la vitesse angulaire. Sans précision dans l'énoncé, je ne pense pas que cette étude soit demandée.
S'il s'agissait d'un pendule simple, l'action de l'air pourrait être modélisée par une force proportionnelle à la vitesse : .
Puisque le pendule étudié ici est un pendule composé, le plus simple est de considérer que l'action de l'air sur l'ensemble du pendule possède un moment par rapport à l'axe de rotation proportionnel à :
.
Le théorème du moment cinétique conduit directement à l'équation différentielle :
On peut aussi s'en sortir en raisonnant sur l'énergie mécanique par cohérence avec l'étude déjà faite en absence de frottement. L'énergie mécanique Em ne se conserve pas en présence de frottements comme tu l'as fait remarquer. Entre deux instants quelconques, sa variation peut s'écrire (voir ton cours) :
où WANC désigne le travail des actions non conservatives entre les deux instants ; WANC < 0.
En dérivant cette expression par rapport au temps, on obtient :
(puissance des actions non conservatives).
Dans le cas d'un solide en rotation autour d'un axe fixe, la puissance d'une action s'écrit :
Pour les forces de frottements, cela donne :
Je te laisse vérifier que tout cela conduit bien à l'équation différentielle fournie au-dessus. Il s'agit sans doute de la résoudre dans le cas de faibles amplitudes. L'équation différentielle peut alors se mettre sous la forme :
Si les frottements sont faibles, cela conduit à un mouvement d'oscillations pseudo-périodique. L'étude de cette équation différentielle est un grand classique de l'enseignement scientifique au niveau (bac+1). En cas de difficulté, tu peux consulter la fiche ci-dessous :
![]()
Dans ton étude la constante K est nulle et tu peux sans doute te limiter au régime pseudo-périodique.
f=- v donc f=-
v donc f=- I(d
I(d /dt)²/2
/dt)²/2
Wanc=f*r Panc=- I(d
I(d /dt)(d²
/dt)(d² /dt²)r. Donc, l'équation du mouvement (d²
/dt²)r. Donc, l'équation du mouvement (d² /dt²)+w²sin
/dt²)+w²sin +
+ I(d
I(d /dt)(d²
/dt)(d² /dt²)a=0
/dt²)a=0
Je ne comprends pas ce que représente -k.(d /dt)² dans Panc/comment le trouver.
/dt)² dans Panc/comment le trouver.
J'ai effectué une démonstration détaillée en m'appuyant sur un résultat de cours : dans le cas d'un solide en rotation autour d'un axe fixe, la puissance est égale au produit de la vitesse angulaire par le moment de la force par rapport à l'axe. Reprend pas à pas mon message précédent...
As tu bien compris la notion de moment de force et la notion de moment de couple ?
"Dans le cas d'un solide en rotation autour d'un axe fixe, la puissance d'une action s'écrit :
P=M_{Oz}.\dot{\theta}
Pour les forces de frottements, cela donne :
P_{ANC}=-k.\dot{\theta}^{2}"
Je n'ai pas compris cette partie et je ne vois pas d'où sort "k".
"dans le cas d'un solide en rotation autour d'un axe fixe, la puissance est égale au produit de la vitesse angulaire par le moment de la force par rapport à l'axe"
Je ne connaissais pas cette définition, I(d /dt)²/2 *F^r ?
/dt)²/2 *F^r ?
Le moment de force: oui je connais la définition mais je ne sais pas trop quand l'utiliser et le moment de couple, je sais pas.
Imagine un pendule simple (masse quasi ponctuelle G au bout d'un fil de masse négligeable comme sur ton schéma) : on pourrait alors définir une force de frottement appliquée à la masse ponctuelle .
Nous avons ici un pendule composé, c'est à dire un solide mobile autour d'un axe horizontal fixe ne passant pas par son centre de gravité (un balancier d'horloge par exemple). L'air exerce donc une action répartie sur toute la surface du pendule, pas une force appliquée en un point précis. Puisque cette action est proportionnelle à la vitesse angulaire, on peut définir un moment de cette action de la forme :
où k est une constante positive dépendant de la forme du pendule. Il s'agit bien sûr d'une modélisation mais elle est pertinente dans la mesure où la courbe expérimentale  =f(t) est conforme à l'équation différentielle obtenue avec ce modèle.
=f(t) est conforme à l'équation différentielle obtenue avec ce modèle.
Concernant la formule :
C'est un classique dont il est facile de trouver la démonstration. En combinant les deux cela donne bien la puissance des actions de frottements :
Je te laisse revoir ton cours sur la dynamique des solides en rotation autour d'un axe fixe.
Et une dernière question, est-ce que quand l'on met sous la forme de l'équation différentielle y"+w02 y =0; w0 est toujours la pulsation propre et plus généralement quand on voit ce terme en coefficient de y, il s'agit de la pulsation propre ?
La pulsation propre est la pulsation théorique de l'oscillateur en absence totale de frottement. Lorsque les frottements sont négligés et que les oscillations sont sinusoïdales, l'élongation théorique vérifie effectivement l'équation différentielle que tu as écrite dans laquelle  o désigne la pulsation propre.
o désigne la pulsation propre.
Bonjour,
De quelle nature est l'énergie cinétique du pendule: énergie cinétique de rotation ou énergie cinétique ?
Étant donnée que l'on néglige la masse de la tige (de longueur l) et je pense que l'on peut considérer que la masse est un point matériel.
En utilisant les coordonnées puis en les dérivants par rapport au temps, on peut trouver la vitesse: Ec(translation)=(1/2).m.v2=(1/2).m.l2.(d /dt)2
/dt)2
Alors qu'en utilisant la formule de l'énergie cinétique de rotation:
Ec(rotation)=(1/2).I0.(d /dt)2 avec I0= m.l2 (théorème de Hyugens: le moment d'inertie d'un objet massique de masse m à une distance l est m.l2) donc Ec(rotation)=(1/2).m.l2.(d
/dt)2 avec I0= m.l2 (théorème de Hyugens: le moment d'inertie d'un objet massique de masse m à une distance l est m.l2) donc Ec(rotation)=(1/2).m.l2.(d /dt)2
/dt)2
Comme l'énergie cinétique de translation...
Et Ec(totale)=Ec(translation)+Ec(rotation)
Hors ce n'est pas le cas
Je pense que tu dois clairement distinguer deux situations, dans le repère d'étude Ro.
1° : le système est assimilé à une masse ponctuelle. Son énergie cinétique est alors et cela, quel que soit le type de mouvement. Il n'y a donc pas à faire la distinction entre une énergie de translation et une énergie de rotation. D'ailleurs, par définition même de l'objet quasi ponctuel, sont énergie cinétique de rotation propre est nulle. S'il n'en est pas ainsi (exemple : très petite bille roulant sur un plan incliné), le solide ne peut pas être assimilé à une masse ponctuelle. Dans le cas du pendule simple, l'énergie cinétique peut s'écrire indifféremment :
2° : le système est un solide de centre d'inertie G. Le théorème de König fournit l'expression de l'énergie cinétique dans le repère Ro. Si on note RG le repère barycentrique (repère de König : repère d'origine G, en translation par rapport à Ro) :
Le premier terme correspond à l'énergie de translation ; le second à l'énergie de rotation mesurée dans le repère barycentrique.