Inscription / Connexion Nouveau Sujet
Pendule
Bonjour,
Je suis actuellement en train de faire un exercice sur un pendule. Aucune information particulière n'est donnée.
J'ai pu faire les 3 premières parties de l'exercice, mais je bloque sur la dernière partie. Elle concerne une étude énergétique.
On lâche la balançoire sans vitesse initiale à partir d'une position Mo telle que  =
= o (
o ( o peut être grand)
o peut être grand)
a) Ecrire la conversion de l'énergie entre la position initiale et une position quelconque.
b) En déduire une relation entre et cos

c) En dérivant cette relation, montrer que l'on retrouve l'équation obtenue en 1.c
J'ai trouvé comme équation à la question concernant la loi de la quantité de mouvement pour la composante tangentielle en 1.c :

=
Voilà, j'espère que vous pourrez m'aider pour ces questions,
En vous remerciant,
Cordialement
a et b)
Delta h = L*(cos(theta) - cos(theta0))
mg.L*(cos(theta) - cos(theta0)) = 1/2.J.w² (conservation de l'énergie mécanique).
mg.L*(cos(theta) - cos(theta0)) = 1/2.m.L².w²
2.g/L*(cos(theta) - cos(theta0)) = w²
2.g/L * (cos(theta) - cos(theta0)) = (d theta/dt)²
-----
c)
En dérivant par rapport au temps :
-2g/L .sin(theta) d theta/dt = 2 d theta/dt * (d² theta/dt²)
Et comme d theta/dt n'est pas identiquement nul, on a :
- g/L .sin(theta) = d² theta/dt²
d²theta/dt² + (g/L) .sin(theta) = 0
-----
Sauf distraction. 
Bonjour,
Tout d'abord, merci beaucoup pour votre réponse
Cependant, j'ai quelques questions,
Je ne comprend pas comment est-ce que l'on obtient : mg.L*(cos(theta) - cos(theta0)) = 1/2.J.w² et pourquoi 1/2.J.w2
Merci 
Soit, un peu autrement :
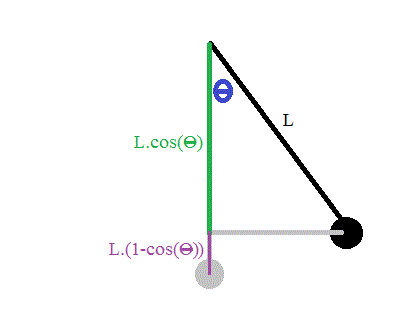
Energie cinétique de la balançoire en theta = theta0 : Ec1 = 0 (puisque la vitesse est nulle en cet endroit)
Energie potentielle en theta = theta0 :Ep1 = mg.L(1-cos(theta0)) (avec le niveau pour les Epp nulle à la position de la balancoire en theta = 0)
E mécanique = EC1 + Ep1 = mg.L(1-cos(theta0))
-----
Energie cinétique de la balancoire en theta quelconque Ec = 1/2.m.v²
Energie potentielle en theta quelconque : Ep = mg.L(1-cos(theta))
E mécanique = 1/2.m.v² + mg.L(1-cos(theta))
-----
Comme les effets des frottement sont négligés, il y a conservation de l'énergie mécanique -->
1/2.m.v² + mg.L(1-cos(theta)) = mg.L(1-cos(theta0))
1/2.v² + g.L(1-cos(theta)) = g.L(1-cos(theta0)
1/2.v² = g.L(1-cos(theta0) - 1 + cos(theta))
v² = 2.g.L(cos(theta) - cos(theta0))
On a v = w*L -->
w²L² = 2.g.L(cos(theta) - cos(theta0))
w² = 2.(g/L).(cos(theta) - cos(theta0))
(d theta/dt)² = 2.(g/L).(cos(theta) - cos(theta0))



