Bien le bonsoir,

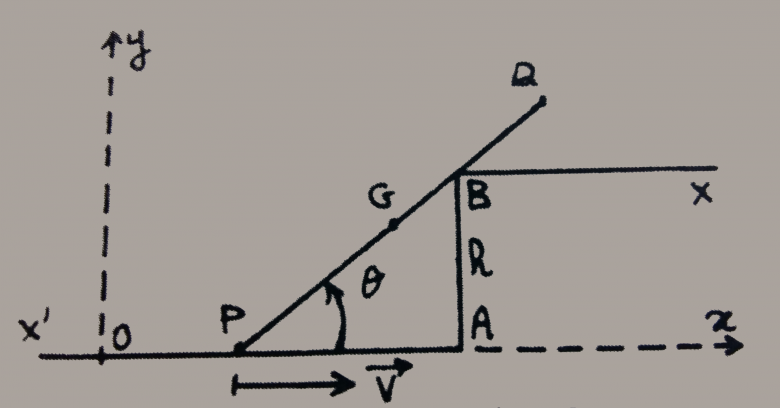
Etudiant en deuxième année de prépa, j'ai quelques soucis sur cet énoncé, et un peu d'aide serai la bienvenu L'exercice considère le schéma attaché à ce post.

On précise :
La barre rectiligne PQ (centre d'inergie = G, longueur = 2L, masse = m, poids = m) glisse sur B sans frottement. P est sur X'A et est poussé vers A avec une vitesse constante V. On appelle "a" la distance OA. On note l'angle = (, ).

Questions : En fonction de , h, L, V et m, calculez :
a) Le vecteur
b) La vitesse G
c) La vitesse de rotation . en fonction de V. Indice : commencer par trouver la dérivée du vecteur = ] -

Avancement:
a) J'ai appelé d la distance PA. J'ai alors défini (d.cos ; d.sin), de manière à écrire = + . A noté que = 1/2 . Je n'ai pas réussi à déterminer en fonction des variables demandées.

b) J'ai commencé par dire qu'un degré de liberté suffisait pour décrire le mouvement de la barre, à savoir l'angle qui augmente jusqu'a /2 (>0). Le mouvement étant dans le sens trigonométrique, on a comme vecteur rotation = - _x.
On peut alors écrire = . Ainsi grâce aux coordonnées trouvée en a), on pourrait trouver .

c) 0/20

Merci !