Inscription / Connexion Nouveau Sujet
Particule guidée
Bonsoir,
Un point A, de masse m, est mobile sans frottement sur un cercle C de centre Ω et de rayon a contenu dans un plan vertical. En plus de son poids, il est soumis de la part du point le plus bas O du cercle à
une force d'attraction dirigée constamment vers O et de module F=kOA, A est toujours en contact avec le cercle C.
1) Exprimer l'énergie mécanique totale Em de A.
C'est sur cette question que je bloque!
Bon pour l'énergie cinétique de A: Ec = 1/2 ma2θ.
2
Pour l'énergie potentielle de pesanteur: Epp = mgz = m.g.a.sinθ
Mais c'est au niveau de l'énergie potentielle dont dérive la force f que je bloque! :S
Merci pour toute aide 
Bonsoir.
On peut écrire F=-kOA (OA en gras est le vecteur OA)
Donc F.dOA=-dEp=-kOA.dOA=-(k/2)*d(OA²)=d(-kOA²/2) d'où Ep=-kOA²/2
On s'est implicitement placé dans le référentiel galiléen de centre 
(ou O, ça n'a pas grande importance).
Dans ce référentiel, O est fixe, donc le déplacement élémentaire est dOA.
En effet, soient P et Q deux points fixes dans le référentiel choisi.
Alors (avec des vecteurs ) :
d(PM)=d(PQ+QM)=d(PQ)+d(QM)=d(QM) car d(PQ)=0 (points fixes)
Il apparaît ainsi que la quantité d(PM) ne dépend pas du point P, tant que P est fixe. On appelle cette quantité le déplacement élémentaire de M dans le référentiel R choisi.
En particulier, O est fixe dans le référentiel R donc dOA est bien le déplacement élémentaire de A dans R.
Si l'on considère O comme centre du référentiel, le déplacement élémentaire ne serait-il pas le vecteur =
? (avec A'=A(t+dt))
Il apparaît ainsi que la quantité d(PM) ne dépend pas du point P, tant que P est fixe. On appelle cette quantité le déplacement élémentaire de M dans le référentiel R choisi.
Je ne comprends plus exactement qu'est ce qu'une circulation infinitésimale ou déplacement élémentaire puisque dans mon cours c'est toujours un vecteur tangent à la trajectoire et dans le sens du mouvement :/
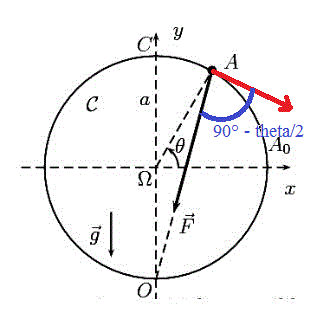
Travail de F :
(En rouge : direction du vecteur déplacement du mobile quand il passe en A ... s'il tourne dans le sens horlogique).
dW = F * a * dtheta * cos(90° - theta/2)
dW = F * a * sin(theta/2) * dtheta
dW = k.OA * a * sin(theta/2) * dtheta
avec :
OA² = a² + a² - 2a².cos(90°+theta)
OA² = 2a² + 2a².sin(theta)
OA² = 2a² (1 + sin(theta))
dW = k.V2 * a² * sin(theta/2) * V(1 + sin(theta)) * dtheta (avec V pour racine carrée)
...
Toutes bêtises incluses.
dW = F * a * dtheta * cos(90° - theta/2)
Pour ma part, dans le triangle ΩOA, je trouve:
D'où
Et l'angle en bleu serait donc égal à 90°−(45°−θ/2) = 45°+θ/2 et non pas à 90°-θ/2 !
C'est donc tout le calcul qui change !
bonjour,
a) la méthode de William est la plus rapide si on sait que: d(
.) = 2 .d
WF = . d
= -k
. d
= -k/2 d(.
) = -k/2 d(OA2)
donc en posant: Ep = k/2 OA2 + Cste
on a bien : WF = -dEp
b) pour le calcul direct, je procéderais ainsi (cf dessin)
dans le repère (,
,
) on a:
= a
+ a r
d = a dO
O (car dr = d
)
donc .d
= a2 dO
.O = a2 cosO dO (car r . O = 0)
d'où WF = -ka2 cosO dO = -d( ka2 sinO)
Ep = ka2sin O + Cste
sauf erreur
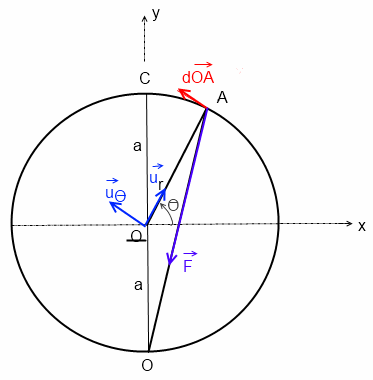
Je ne comprends plus exactement qu'est ce qu'une circulation infinitésimale ou déplacement élémentaire puisque dans mon cours c'est toujours un vecteur tangent à la trajectoire et dans le sens du mouvement :/
C'est bien ça.
Le plus naturel est de dire que le déplacement élémentaire vaut AA' (imaginer la flèche du vecteur). Mais ce n'est pas toujours le plus pratique, notamment ici.
En effet, on peut écrire : AA'=AO+OA' = OA'-OA
Ou alors en considérant que le mobile est à la position A à la date t, et en A' à t+dt, alors on peut écrire A=M(t), A'=M(t+dt)
Donc AA'=OM(t+dt)-OM(t) = dOM, valable pour tout point O fixe du référentiel.
Annuler
connectez vous