Inscription / Connexion Nouveau Sujet
Oscilloscope numérique, fonction de transfert, Bode
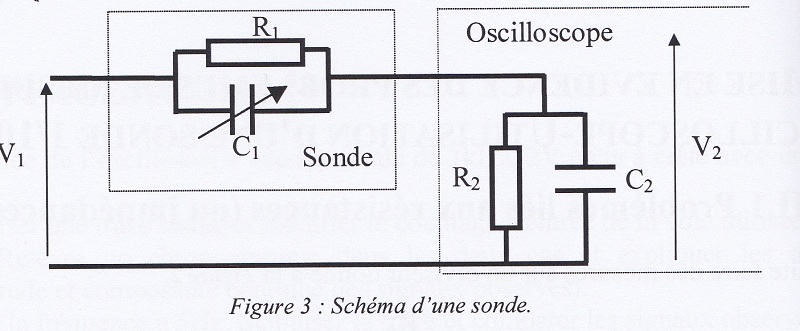
Bonjour, voilà j'ai un exercice sur les oscilloscopes et je vous avouerai que j'ai un peu de mal avec les fréquences de coupures et les diagrammes de Bode... voici mon schéma :
Dans un premier temps, je dois déterminer ma fonction de transfert V2(j )/V1(j
)/V1(j )
)
J'ai donc calculé ceci et je trouve :
H (j ) = (R2 / (1 + jR2C2
) = (R2 / (1 + jR2C2 )) / (R2 / (1 + jR2C2
)) / (R2 / (1 + jR2C2 ) + R1 / (1 + jR1C1
) + R1 / (1 + jR1C1 ) )
) )
2ème question : Les fréquences de coupure seront expromées en posant, R2 = kr * R1 et C2 = kc * C1 . Donner les différents diagrammes asymptotique de Bode pour kr < 1/kc , kr > 1/kc , et kr = 1/kc Préciser dans les différents cas les valeurs de gains aux cassures des courbes.
là je bloque sur les fréquences de coupures et les diagrammes de Bode je n'en ai jamais tracé...
En espérant que quelqu'un puisse m'aider,
Cordialement
ton calcul de H me semble juste. Par contre on ne laisse jamais ça sous cette forme. Il faut simplifier jusqu'à n'avoir qu'un trait de fraction. Quelque chose du type : H(jw) = Q(jw) / P(jw) où Q et P sont des polynomes.
ça t'aidera à tracer le bode
j'obtiens ceci :
[[R2(1 - R1R2C1C2 2 + j(R1C1
2 + j(R1C1 + R2C2
+ R2C2 )]] / [[ (1 + jR2C2
)]] / [[ (1 + jR2C2 )(R1 + R2 + j(R1R2C2
)(R1 + R2 + j(R1R2C2 + R1R2C1
+ R1R2C1 )) ]]
)) ]]
C'est bon comme ça ou je dois multiplier par le conjugué du dénominateur ?
J'ai un peu adapté le calcul pour avoir P(w) et un Q(w)
soit :
[ - 2(R1R22C1C2) +
2(R1R22C1C2) +  (jR1R2C1 + jR22C2) + R2 ] / [ -
(jR1R2C1 + jR22C2) + R2 ] / [ - 2(R1R22C22 + R1R22C1C2) +
2(R1R22C22 + R1R22C1C2) +  (2jR1R2C2 + jR1R2C1 + jR22C2) + R1 + R2 ]
(2jR1R2C2 + jR1R2C1 + jR22C2) + R1 + R2 ]
Mais comme le calcul précédent il est aussi à rallonge...
je ne vois pas comment tu fais pour obtenir ça.
Moi j'ai :
H(jw) = R2.(1+jwC1R1)/(R1+R2+jw.R1.R2.(C2+C1))
En fait quand j'ai ça
H (j) = (R2 / (1 + jR2C2 )) / (R2 / (1 + jR2C2
)) / (R2 / (1 + jR2C2 ) + R1 / (1 + jR1C[sub]1[/sub
) + R1 / (1 + jR1C[sub]1[/sub ]) )
]) )
je mets les deux fractions du dénominateur au même dénominateur d'où le calcul à rallonge...
j'ai trouvé d'où venait l'erreur, j'avais pris Zc = 1 / jC , après rectification j'arrive bien au même résultat que vous !
, après rectification j'arrive bien au même résultat que vous !
Ensuite : Les fréquences de coupure seront exprimées en posant, R2 = kr * R1 et C2 = kc * C1 . J'imagine que je dois remplacer dans la fonction H(jw) calculé juste au dessus non ?
J'obtiens pour R2 = kr * R1
H(jw) = [kr ( 1 + j R1C1)] / [ 1 + kr + j
R1C1)] / [ 1 + kr + j krR1(C1 + C2)]
krR1(C1 + C2)]
Mais j'ai l'impression de ne pas répondre à la question, pour moi la pulsation de coupure est Wc= 2 Fc... là apparemment on a plusieurs fréquences de coupures...
Fc... là apparemment on a plusieurs fréquences de coupures...
tu as un premier ordre en haut et un premier ordre en bas. C'est pas difficile de tracer les deux courbes, puis les superposer dans les 3 cas différents
Mais pour la fréquence de coupure on attend de moi plusieurs fréquences si j'ai bien compris non ? Quelles sont donc ces fréquences ? Puis pour le diagramme, je ne sais pas si Kr est plus grand ou plus petit que Kc ça n'a pas d'importance si ? Et le diagramme en ordonnée je mets le module de H et en abscisse l'argument ou bien en ordonnée le gain et en abscisse  ? j'imagine le gain ainsi que la pulsation afin de relever le Gain aux cassures est-ce bon ?
? j'imagine le gain ainsi que la pulsation afin de relever le Gain aux cassures est-ce bon ?
Je ne comprends plus rien... d'où sort ce 1/(1+k.jw) ? et je n'ai jamais tracé de fonction complexe, placer un point du type a + ib sur un graphe je sais faire, en revanche tracer une fonction je ne sais pas, comme j'ai dit plus haut je n'ai jamais tracé de diagramme de Bode pour le Gain en ordonnée j'arrive à
Gb = 20 log ( [ (R2² + w²C1²R1²R2²)] / [
(R2² + w²C1²R1²R2²)] / [  ((R1+R2)² + w²R1²R2²(C1+C2)²)] ...
((R1+R2)² + w²R1²R2²(C1+C2)²)] ...
arrête ces calculs compliqués.
ceci est le bode d'une fonction de transfert du type H(jw) = 1/(1+jw/wc) non ?
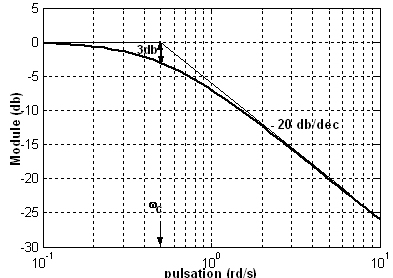
Je n'en ai jamais étudié donc j'ai du mal à dire oui... Je pose en réalité pour votre exemple : H(x) = 1 / (1+x/ c) si c'est ça je pense pouvoir tracer le diagramme, à condition d'avoir des valeurs... dans mon exercice on me demande de calculer la fonction de transfert, ce que j'ai fait, puis les fréquences de coupures... comment puis je en déterminer plusieurs ? je pose Module de |H(jw)| = 1 /
c) si c'est ça je pense pouvoir tracer le diagramme, à condition d'avoir des valeurs... dans mon exercice on me demande de calculer la fonction de transfert, ce que j'ai fait, puis les fréquences de coupures... comment puis je en déterminer plusieurs ? je pose Module de |H(jw)| = 1 /  2 , cela est tout le temps valable ? Puisque j'ai du
2 , cela est tout le temps valable ? Puisque j'ai du  ² dans le module j'en déduis 2 pulsations de coupure est-ce bon ?
² dans le module j'en déduis 2 pulsations de coupure est-ce bon ?
Une fois que j'ai mes pulsations de coupure (d'ailleurs à quoi vont elles me servir pour le tracé de Bode ?) je trace pour les 3 cas différents kr >,<,=, 1/kc le diagramme, mais je n'ai pas de valeurs pour ces "k", cela va-t'il me poser un problème ?
les pulsations de coupure sont là où les asymptotes se coupent (en wc quoi)
si tu ne sais même pas tracer un premier ordre passe-bas tu vas avoir du mal à continuer ...
mon but est d'apprendre à tracer ces diagrammes quand j'aurai pris la main je suis sûr que ça ira ! je regarde quelques topics sur le net portant la dessus mais tous traitent des problèmes beaucoup plus faciles...
En posant |H(jw)| = 1 /  2
2
j'arrive à :
0 = -1/2 + Kr - (1/2)Kr² + (1/2) ²R1²Kr²C1²(-1 + Kc + Kc²)
²R1²Kr²C1²(-1 + Kc + Kc²)
Est-ce bon ? Je n'ai pas de valeurs pour Kc et Kr dois je utiliser les conditions c'est à dire Kr<1/Kc ou Kr>1/Kc et Kr=1/Kc ?
H(jw) = [kr ( 1 + jwR1C1)] / [ 1 + kr + jwkrR1(C1 + C2)]
donc H(jw) = kr/(1+kr) . ( 1 + jwR1C1) / [ 1 + jw.(kr/(1+kr)).R1(C1 + C2)]
écrivons ça comme ça. Si tu regardes le dénominateur et que tu identifies à ce que je t'avais donné comme modèle de premier ordre (1/(1+jw/wc) ) alors tu trouves une pulsation de coupure : wc = (1+kr)/(kr.R1(C1 + C2))
Donc je n'ai qu'une fréquence de coupure ? Fc =  c/2
c/2 , d'accord ! Pour le diagramme me suffit juste de remplacer les valeurs R2 = kr * R1 et C2 = kc * C1 dans ma fonction, puis de calculer le module et après en ordonnée j'ai 20 Log (Module) et en abscisse w, à priori ça devrait être bon pour le tracé ! Je vais encore regarder et refaire des exemples pour voir si j'ai bien entravé ! Merci beaucoup pour le temps que vous m'avez consacré afin de m'aider à mieux comprendre le sujet !
, d'accord ! Pour le diagramme me suffit juste de remplacer les valeurs R2 = kr * R1 et C2 = kc * C1 dans ma fonction, puis de calculer le module et après en ordonnée j'ai 20 Log (Module) et en abscisse w, à priori ça devrait être bon pour le tracé ! Je vais encore regarder et refaire des exemples pour voir si j'ai bien entravé ! Merci beaucoup pour le temps que vous m'avez consacré afin de m'aider à mieux comprendre le sujet !


