Inscription / Connexion Nouveau Sujet
Oscillations forcées
Bonjour,
Je rencontre des difficulté sur le début d'un problème de mécanique.
Une voiture roule sur un sol ondulé d'équation .
On considère que la distance entre les roues est un multiple de L, donc les 2 roues sont toujours à la même cote.
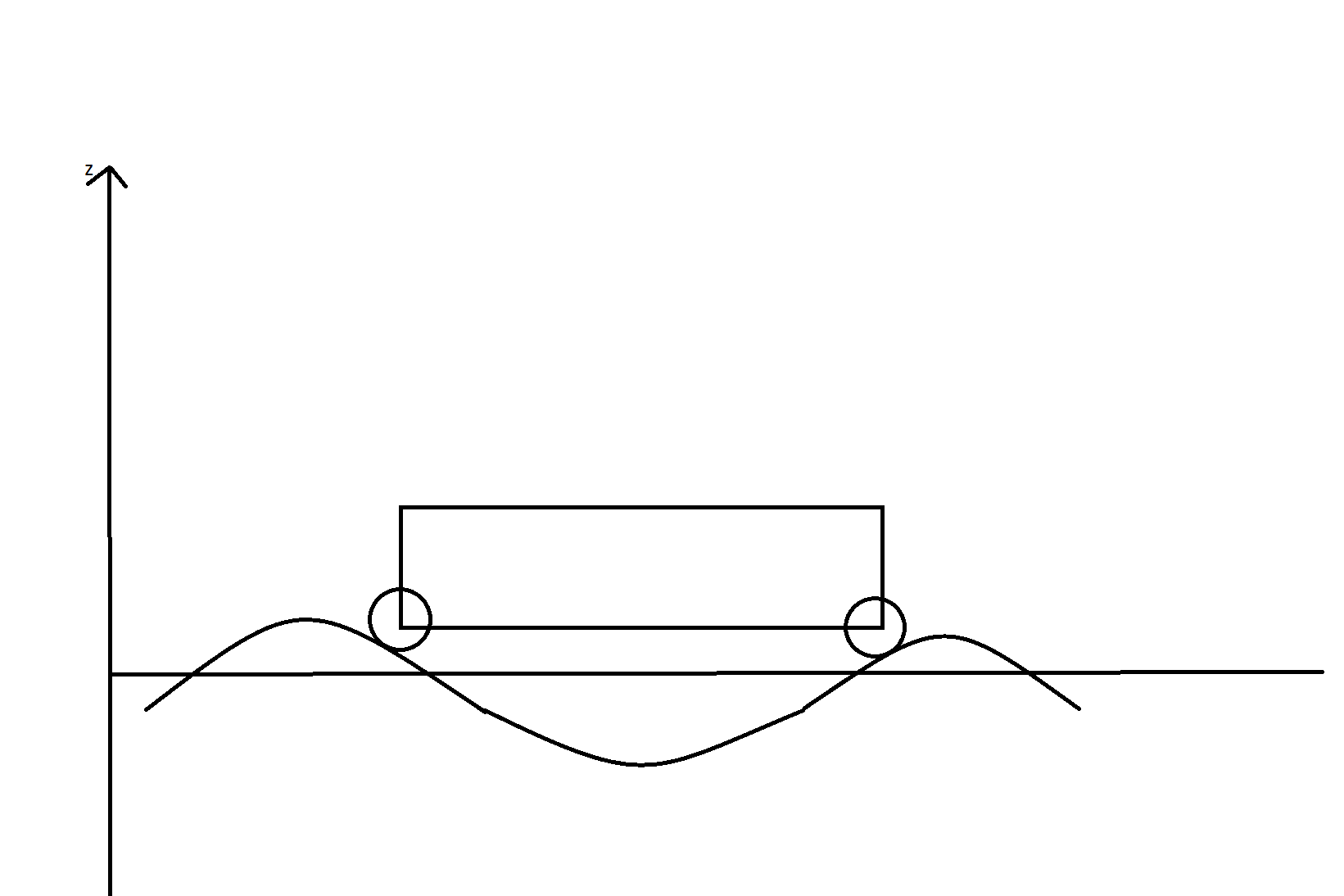
La voiture possède des suspensions dont les points d'attache sont de même cote que G (voir schéma).
Sur un sol plat l'allongement de la suspension par rapport à la position d'équilibre est :
où est la cote du centre d'inertie de la voiture et
sa cote à l'équilibre.
1) Que devient l'expression de Z sur sol ondulé ?
Ce que je ne comprends pas : normalement sur sol plat les suspensions ne travaillent pas donc ne devrait-on pas avoir Z = 0 ?
Sur sol ondulé comment exprimer Z ?
Merci beaucoup pour votre aide
Bonjour
A l'équilibre l'action des ressorts de suspension compense juste le poids du véhicule :Z=0 .
Lorsque le véhicule oscille verticalement tout en roulant , le ressort s'allonge de Z si le véhicule se soulève légèrement vertical pendant que simultanément, il se raccourcit de zsol. le ressort d'une suspension exerce donc une force verticale dont le projeté sur l'axe (O,z) vertical ascendant est de la forme :
L'étude du mouvement vertical du véhicule va bien te conduire à étudier un oscillateur soumis à une force d'excitation périodique si la vitesse horizontale V du véhicule par rapport au sol peut être considérée comme constante.
Le régime d'oscillations forcées est le régime particulier où l'oscillateur oscille à la même pulsation que l'excitateur. Cela va amener à étudier des solutions de la forme :
J'ai raisonné en imaginant une seule suspension équivalente aux quatre suspensions du véhicule. Cela sous toutes réserves bien sûr : n'ayant pas l'énoncé intégral ni le schéma...
Merci beaucoup pour votre réponse et vos précisions !
Donc l'allongement du ressort est à tout moment mais quelle est l'expression de Z ? C'est la que se situe mon incompréhension je penses :/
D'après ce que j'ai compris : si h est l'altitude à l'équilibre du centre de gravité du véhicule par rapport au sol horizontal ou par rapport au niveau moyen du sol ondulé, l'altitude de ce centre de gravité à une date t quelconque quand le véhicule oscille verticalement est (h+Z). A l'équilibre, le ressort est comprimé pour compensé le poids du véhicule. Par rapport à cet état comprimé, le ressort est allongé de (Z-zsol) à la date t.
Toujours sous toutes réserves...


