Inscription / Connexion Nouveau Sujet
Oscillations amorties : la balançoire
Bonsoir, j'ai quelques difficultés à résoudre cet exercice :
Un enfant de masse 25 kg est assis sur une balançoire. Son centre d'inertie est à la distance de 3m de l'axe de rotation horizontal.
On pousse l'enfant jusqu'à ce que les cordes fassent un angle de 40° avec la verticale puis on cesse de le pousser.
Après 4 oscillations, l'amplitude du mouvement n'est plus que de 25°.
Calculer le travail moyen des forces de frottement par oscillation.
On prendra g= 10m/s^-2
J'ai essayé d'appliquer le théorème de l'énergie cinétique, mais on ne connait pas la vitesse finale ainsi que les angles intermédiaires durant les 4 oscillations donc je ne voit pas trop par où commencer... 
Merci d'avance à ceux qui voudront bien se pencher dessus 
bonsoir,
comme toujours il faut faire un dessin! (voir plus bas)
position de départ: A
position d'arrivée: B (après 4 oscillations)
la vitesse en A est ...
la vitesse en B est ...
on connait les angles et la longueur OA=OB donc on connait h
donc on connait la variation d'énergie mécanique entre les positions A et B.
on sait par ailleurs que: Em = travail des forces dissipatives
Em = travail des forces dissipatives
donc l'exo est fini 
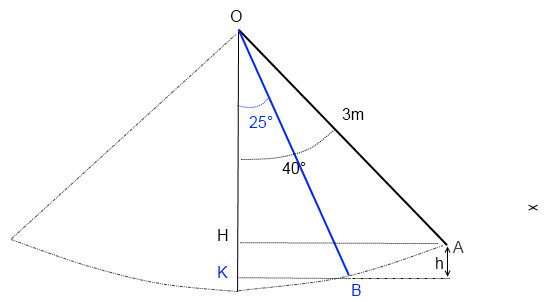
Edit Coll : image recadrée
J'ai calculé W(F)= mgh = 25.10.3(cos40-cos25) = -105 J
La réponse donnée était -26 J, j'ai du mal à comprendre d'où vient l'erreur...


