Bonsoir
Tu trouveras à l'aide du lien ci-dessous une démonstration de la raideur équivalente à deux ressorts de masses négligées associés en série, paragraphe 3. Pose ensuite des questions complémentaires si tu le juges utile.

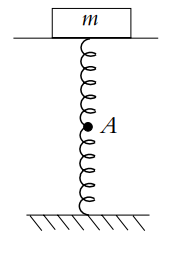
Bilan des forces de la solution :

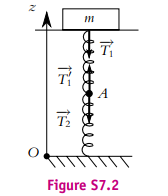
Les grandeurs relatives au ressort du haut (respectivement du bas) sont indicées par 1 (respectivement 2). On note
le vecteur unitaire de l'axe Oz. Sur la figure (S7.2) on n'a pas représenté le poids pour plus de clarté. Les forces s'exerçant sur la masse m sont : son poids m et
la tension = −k1(l₁ − l₀₁)
. Les forces s'exerçant sur le point A sont les deux tensions = −k2(l2 − l₀₂)
et = (les ressorts sont de masse négligeable).
Mon premier blocage se situe au niveau de la représentation de . Selon moi il devrait être orienté vers le haut car la masse tend à raccourcir le ressort.

Une force caractérise l'action d'un corps 1 sur un corps 2. Sans ces deux précisions,il y a toujours ambiguïté. Tu as raison si T1 désigne l'action du ressort sur la masse.
Telle que les vecteurs sont représentés, T1 est l'action de la masse sur le ressort 1 et T'1 l'action du ressort 2 sur le ressort 1. L'application de la RFD à ce ressort de masse négligeable conduit à une somme vectorielle nulle de ces deux forces. Lis attentivement le document que je t'ai fourni.

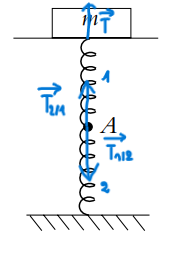
Pas vraiment. Il faut garder les vecteurs forces du schéma original fourni le  02-10-25 à 21:47 mais , quoi qu'en dise ton document, il est destiné à l'étude des ressorts, pas du mouvement de la masse.
Tu choisis d'abord comme système le ressort 1 seul. Son poids étant négligé, les deux forces extérieures sont comme je l'ai déjà écrit :
1° l'action T1 de la masse
2° l'action T'1 du ressort 2.
Ces deux forces ont les sens précisés sur le schéma du  02-10-25 à 21:47. Le principe fondamental de la dynamique appliqué à ce ressort 1 de masse négligeable conduit à ces deux vecteurs opposés.
T2 désigne l'action du ressort 1 sur le ressort 2. Ce vecteur est l'opposé de T'1 : principe des actions réciproques.
La suite est facile.

T1/2 est l'action du ressort 1 sur 2 et T2/1 est l'action du ressort 2 sur 1.
La relation fondamentale appliquée à m en projection sur Oz :
m= −k1(l1 − l₀₁) − mg
et pour A (masse mA nulle) :
mAA = 0 = k1(l1 − l₀₁) − k2(l2 − l₀₂)

La masse de chacun des ressorts est négligée. Je me re-re-répète : le système d'abord étudié est le ressort n° 1 (celui du haut) et on s'intéresse uniquement aux deux forces exercées par l'extérieur sur ce ressort 1. Dans l'application du principe fondamental à ce ressort 1, il faut poser m1=0 ! Cela conduit immédiatement à T1 et T'1 : deux vecteur opposés donc de même norme.

Pour le système ressort (1), en appliquant le RFD on a
T₁=T₂₍₁₎=k₂(l₂-l₀₂)
Pour le point A sans masse, on a : k2(l₂-l₀₂)=k1(l₁-l₀₁)
Sur le système masse m en appliquant le RFD on a : -mg-k1(l1-l01)=m et comme ce sytème doit être équivalent à -mg-k_e(l_e-l_0e)=m, puisque l₂=, alors on a :



Et donc par identification on a : k_e=k1k2/k1+k2

On a de même:

Après résolution on trouve:

C'est la démonstration qui t'est proposée ? Pourquoi pas mais il y a tout de même plus simple en réfléchissant à ce qu'est le ressort équivalent (un peu plus de réflexion, un peu moins de calculs) : même longueur à vide : et même variation de longueur l_e=l₁+l₂ quand il est soumis à une même force extérieure T.
Le plus difficile à démontrer est que T représente à la fois la tension du ressort équivalent, la tension du ressort 1 et la tension du ressort 2. De l_e=l₁+l₂ , on déduit :



et puisque :

Désolé pour ce retard, j'avais eu quelques soucis.
Merci pour cette méthode courte et élégante.

Pas très précis et rigoureux, ton dernier message. Je pense avoir fourni une démonstration rigoureuse assez simple sur le document que je t'ai indiqué en appliquant la relation fondamentale à un ressort dont la masse est négligée puis en appliquant le principe des actions réciproques, aussi appelé principe de l'action et de la réaction ou encore troisième loi de Newton.
Attention aux sens des vecteurs par rapport à ton problème. Dans mon document les ressorts sont allongés par rapport à leurs longueurs à vide alors qu'ils sont comprimés dans ton problème. Cela inverse les sens des vecteurs forces.

Je n'ai pas vu le document dont vous parlais. Il a été épinglé ?
Donc en représentant toutes les forces, celles de la masse et des ressorts on a d'une part T(masse sur ressort)=T(2 sur 1)d'après le principes des actions réciproques. Et d'autre part, T(1 sur 2)=T(2 sur 1) et comme T(masse sur ressort)=T(ressort sur masse)=ke(le-l0e)
Alors on déduit que les ressorts 1 et 2 sont soumises à la même tension T.
C'est bien cela ?

Je n'ai pas vu le document dont vous parlez. Il a été épinglé ?
Donc en représentant toutes les forces, celles de la masse et des ressorts on a d'une part T(masse sur ressort)=T(2 sur 1)d'après le principes des actions réciproques. Et d'autre part, T(1 sur 2)=T(2 sur 1) et comme T(masse sur ressort)=T(ressort sur masse)=ke(le-l0e)
Alors on déduit que les ressorts 1 et 2 sont soumis à la même tension T.
C'est bien cela ?

Ok. Je crois que tu as bien compris maintenant.

Merci pour votre aide