Inscription / Connexion Nouveau Sujet
Oscillateurs basse fréquence
Bonjour,
Tout d'abord, bonne année à toutes et à tous. Meilleurs voeux.
Je suis donc en face d'un exercice sur les oscillateurs, et malgré la lecture je n'ai à vrai dire toujours pas compris ça marche. Surtout dans la détermination de A et B ...
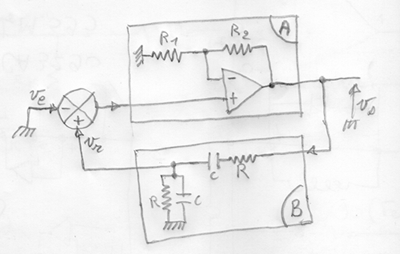
Voici le problème. Si jamais vous connaissez un cours assez bien détaillé, n'hésitez pas à me l'envoyer, merci.
***Image recadrée, la partie texte est à recopier***
Bonjour,
Surtout dans la détermination de A et B
???... A et B, c'est quoi ?
Très classique... C'est un oscillateur à pont de Wien.
Ce montage oscille s'il a un gain suffisant (déterminé par R2 et R1) parce qu'il y a un rebouclage de la sortie sur l'entrée +. Donc il ne s'agit pas d'une contre-réaction mais d'une réaction...
Il faut d'abord calculer la tension v+ par rapport à vs (tension en N).
Quelques généralités sur ce montage :
RC série : Z2 = R + 1/(jwC) = (1 + jwRC)/(jwC)
RC parallèle : Z1 = (R * 1/(jwC))/(R + 1/(jwC)) = R/(1+jwRC)
VM = VN * Z1/(Z1+Z2)
VM = VN * jwRC/(1+3jwRC+j²w²R²C²)
V- = VN * R1/(R1+R2)
VM = V- -->
VN * jwRC/(1+3jwRC+j²w²R²C²) = VN * R1/(R1+R2)
jwRC/(1+3jwRC+j²w²R²C²) = R1/(R1+R2)
(R1+R2).jwRC = R1.(1+3jwRC+j²w²R²C²)
jwRC.R2 = R1.(1+2jwRC+j²w²R²C²)
-----
Si R2 = 2R1, on a : 1 - w²R²C² = 0, w = 1/(RC)
On a alors VM = VN * jwRC/(3jwRC)
VM = VN/3
Le montage oscille donc à la fréquence f = 1/(2.Pi.R.C)
CEPENDANT : ce montage est tigneux, il y a oscillation si R2 = 2R1.
Mais si on a pile ce rapport (R1 = 2R1) l'amplitude de l'oscillation n'est pas définie.
Si le rapport R2/R1 n'est pas tout à fait égal à 2, soit l'amplitude diminue d'amplitude et s'arrête, soit l'amplitude augmente et la sinusoïde est alors fortement déformée par la saturation de l'ampli.
Si on veut que cela fonctionne correctement, on introduit souvent pour R2 ou R1 un composant non linéaire ... mais c'est une autre histoire.
Sauf distraction. 
Merci de vos réponses, mais moi le problème réside déjà dans l'identification juste dans le schéma propre de A et B ...
Parce-que dans le cours, ils utilisent le fait que A.B = 1, mais bon je suppose c'est la même que ce qu'à fait JP.
Merci encore,
Oui, A et B... Souvent, on les appelle G et H mais peu importe... Je comprends...
Il s'agit d'identifier ce schéma avec le schéma général de la réaction. Il se trouve que c'est assez facile sur ce schéma.
A est le gain de la chaîne directe. Donc :
B est le gain de la chaîne de réaction. Donc :
Merci, du coup c'est pas plutôt 1 + R1/R2. Je crois je commence à comprendre. Pour généraliser, on pourrait avoir pour A (complexe) tout le temps : V-/Vn et B : V+/Vn ?
Et d'où est venue votre intuition pour supposer si R2=2R1 on a oscillation ?
Non, c'est bien
Pour généraliser, on pourrait avoir pour A (complexe) tout le temps : V-/Vn et B : V+/Vn ?
Non, c'est un peu plus compliqué que ça... Il faut comparer le schéma général de la réaction avec le schéma que l'on a. Sur celui-ci, c'est facile mais sur d'autres, c'est plus difficile...
R2 = 2 R1... Ce n'est pas une intuition. C'est le résultat du calcul. Cela vient de AB = 1 d'ailleurs. On peut aussi prendre le gain total du montage.
Pour
J'ai vraiment pas d'exemple du schéma de base ... Pouvez vous m'en montrer un ? Du coup je ne vois pas pourquoi c'est A = 1+R2/R1