Inscription / Connexion Nouveau Sujet
Oscillateur simple
Bonjour j'ai un long exercice et cela va me prendre beaucoup de temps à le recopier savez vous si je peux le prendre en photo?
Salut,
Non, tu ne peux-pas.
Seuls les dessins peuvent être envoyer sur le site ... mais le texte doit être recopié.

On considère un oscillateur simple constitué d'un ressort horizontal de longueur à vide
l0=30 cm et de constant de raideur k=20 N.m-1.
L'extrémité O de ce ressort est fixée à un bâti fixe dans le référentielle du laboratoire. L'autre extrémité est fixée à une masselotte de masse m=500 g sur une tige horizontal
A t =0 on allonge le ressort d'une longueur a=20 cm par rapport à sa longueur d'équilibre
l0 et on lâche sans vitesse initial.
Etude dynamique :
déterminer la dimension de la constant de k en fonction des dimensions fondamentales.
Quelle est son unité légale?
Que représente physiquement cette grandeur?
exprimer la force de rappel en fonction de x(t)
déterminer l'équation différentielle.
On pose
Exprimer numériquement la période d'oscillations.
Pour le moment j'aimerais répondre à ces question je donnerais la suite des questions après?
Réponse:
1-1. K est en Newton/m
Les newtons représente une force donc on à Newton=m/s²
On a donc des m²/s²
1-2
physiquement cette grandeur représente une accélération * des mètre (je sais pas si il y a plus précis)
Et pour la suite je bloque
Bonjour,
Non il y a un problème pour la question 1-1.
En effet la constante de raideur c'est à dire des Newton par mètres. (ici l est une longueur en mètres).
Cependant 1 Newton = 1 donc en remplaçant dans k on trouve
De plus avec la formule donnée dans l'énoncé:
on retrouve aussi directement la bonne unité pour k on se rappelant que
est en
.
Pour la suite de l'exercice, il s'agit simplement de l'application de la relation fondamentale de la dynamique (2ème loi de Newton si tu préfères) dans le cas d'un mouvement à une dimension. Donc en faisant un bilan des forces et en constatant que deux de ces forces vont se simplifier tu auras une expression simple en se souvenant de la relation donnant la force de rappel. Et bien sûr l'origine du repère pourra être placé exactement à la longueur d'équilibre et ainsi sera simplement la position donnant l'écart à l'équilibre.
Est-ce bon ?
Cela est certainement dans le cours.
Mais en principe tu as l'expression: en décidant que le mouvement se réalise suivant l'axe (Ox). Ici
est la longueur à vide et l est la position de ton point par rapport à l'origine. Mais comme je l'ai proposé tu peux très bien choisir
en déplaçant le repère sur la position d'équilibre pour te simplifier la vie.
Comment redémontrer la force de rappel
voila ce que j'ai en shéma
Bilan des force:
et ensuite comment je peux retrouvé la force de rappel?
Salut,
Attention, qu'on demande une analyse dimensionnelle.
F = - k.Delta L
k = -F/(Delta L)
[k] = [F]/[Delta L]
Or [F] = MLT^-2 (masse * accélération)
et [Delta L] = L
--> [k] = MLT^-2/L
[k] = MT^-2 (c'est la dimension de k)
L'unité légale ... cela ne veut pas dire grand chose, on peut tout aussi bien utiliser (dans le système SI) le "N/m" que le "kg/s²"

Bonjour J-P
Oui en effet et en plus avec cette unité l'interprétation physique est bien plus simple. Mais dans ma tête je revenais aux unités de bases du SI en faite.
Quant au bilan des forces il est un peu étrange, -g n'est pas une force par exemple.
Tu voulais sans doute parler du poids : . En effet le poids intervient mais il est compensé par l'interaction du support. De plus il faut certainement négligé les forces de frottements du support. C'est certainement indiqué dans l'énoncé.
Donc à la fin il ne reste que la force de rappel.
Tu ne vas pas retrouver la force de rappel, tu l'utilises dans la relation fondamentale de la dynamique, donc suivant l'axe (Ox) tu as simplement:
Maintenant il faut faire intervenir x dans la force de rappel comme je l'ai déjà expliqué par changement de repère par exemple et tu devrais tomber sur l'équation différentielle d'un oscillateur harmonique (car pas de frottements).
Il faut bien les unités SI en effet:
-k(l-l0)=ma
et si on le projet selon l'axe de x on obtient:
-kx(t)=ma?
Je me suis borné à répondre à ceci;
"déterminer la dimension de la constant de k en fonction des dimensions fondamentales.
Quelle est son unité légale? "
Et je l'ai traité dans le cas général : F = -k.Delta L
Et ceci est valable quelle que soit la nature de F.
Je n'ai pas lu la suite de l'exercice.

Oui ce qui me perturbe est le terme "fondamentales". Donc je revenais vraiment aux unités de bases mais quand on regarde la question qui suit sur l'interprétation il est vrai que manipuler des N/m est beaucoup plus simple donc c'est certainement la réponse attendue...
Oui en effet et comme l'accélération est la dérivée seconde de la position tu as:
Il faut maintenant écrire cette équation sous une forme correcte pour se ramener à l'équation générale d'un oscillateur harmonique et il faudra la résoudre... Je te laisse faire, normalement c'est dans ton cours.
Tu veux certainement parler de l'équation caractéristique et non de l'équation différentielle attention.
Oui tu peux passer par là mais la solution est très connue c'est une expression en cosinus, je te laisse chercher.
Mais avant ça tu peux identifier l'equation générale avec l'équation que tu obtiens pour déterminer
C'est immédiat :
x" + wo².x = 0
x = A.sin(wo.t) + B.cos(wo.t)
ou si on préfère :
x = C.cos(wo.t + Phi)
Sauf distraction. 

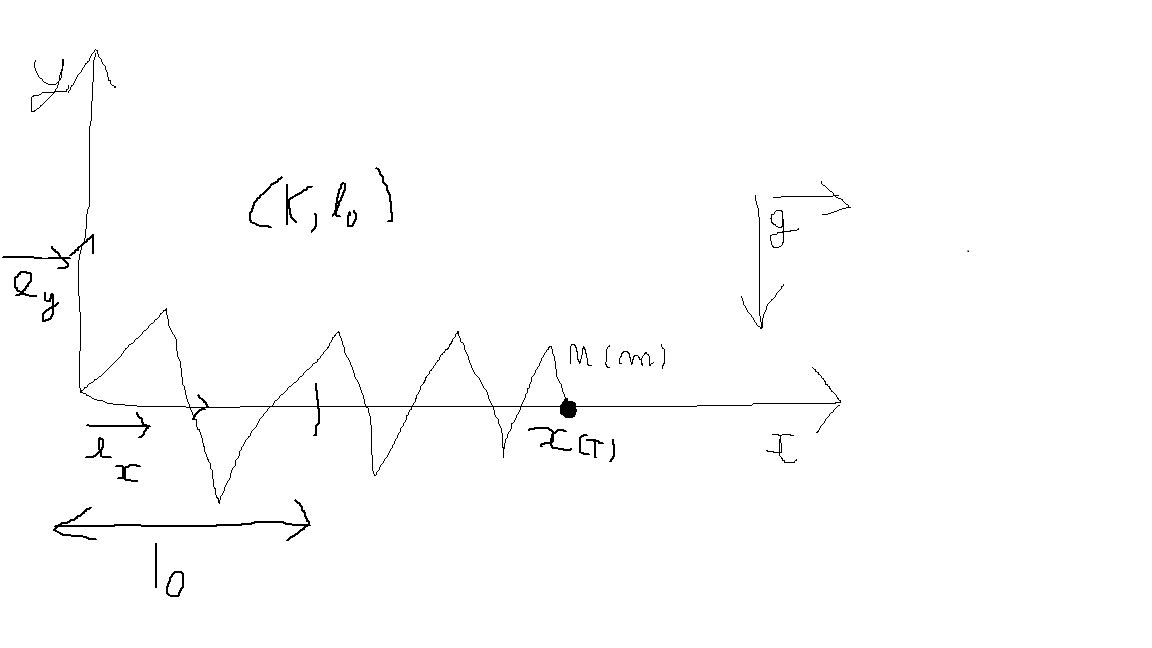
 mais comment?
mais comment? 
