Inscription / Connexion Nouveau Sujet
Oscillateur mécanique excité
Bonsoir,
Je suis en train d'étudier les oscillateurs mécanique et je bloque sur mon premier exercice. La première question consiste à montrer que l'équation différentielle est bien celle indiquée par l’énoncé. Je me permets de mettre une image de l'énoncé comportant un schéma et des formules/notations complexes
Concernant la première question, je suppose qu'il faut se placer en régime sinusoïdal forcé et appliquer le PFD. Cependant il y a un frottement fluide et l'oscillateur est vertical, comment commencer dans le cas d'un oscillateur mecanique excité et non harmonique ?
Si vous pouviez m'indiquer la démarche pour débuter, je vous remercie.
Cordialement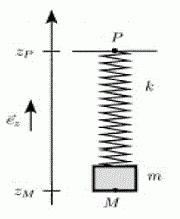
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
On considère l'oscillateur mécanique ci contre, composé d'une masse m et d'un ressort de raideur k, l'ensemble étant suspendu au point P. La cote zm du point M situé à la base de la masse est notée z0+ ou z0 est la cote de la position d'équilibre de M lorsque P est fixe en P0. Ce point P est animé autour de P0 d'un mouvement sinusoidal vertical, imposé par un vibreur et donné par a(t)=a0cos(wt) (w pour omega) avec a0>0. On suppose de plus que la masse m est soumise à une force de frottement fluide de type visqueux
et
1)Montrer que l'équation différentielle du second ordre vérifiée par delta(t) s'écrit :
bonsoir,
il suffit d'appliquer le PFD à la masse m
tu connais les forces: P, F et la force de rappel du ressort est aussi connue puisqu'on connait l'allongement du ressort à l'instant t en fct de a(t), de  (t) et du reste
(t) et du reste
Merci pour votre réponse, est ce correct ?
On se place dans le référentiel terrestre
la masse n'est sur aucun support
normalement, vu que c'est vertical, la masse est soumise à son poids+ force ressort + frottement mais dans notre cas on travaille avec delta qui est une oscillation autour de la postion d'équiliblre.
zm=z0+delta. z0 est defini comme la position d'équilibre, P ne bouge pas. 0=k(zp-z0-l0)-mg
Donc m*delta''=k(zp+a(t)-z0-delta-l0)-mg-beta*delta'*beta*delta'
il reste m*delta''=k(a(t)-delta(t))-beta*delta'
Pourquoi ne doit on pas négliger le poids ? Sans le négliger nous ne retrouvons pas l'équa diff proposées après application du pfd
négliger quel poids? celui du ressort ou celui de m
on néglige déjà le poids du ressort donc si on néglige aussi m il ne se passera plus grand'chose mécaniquement parlant, non?
Celui de la masse ce qui revient à traiter un oscillateur horizontal sans poids, je ne vois pas comment obtenir l'ewua diff sans le negliger :/


