Inscription / Connexion Nouveau Sujet
Oscillateur harmonique : système masses-ressort
Bonjour,
Je rencontre des difficultés dans le cadre d'un exercice sur les oscillateurs harmoniques.
Voici le sujet :
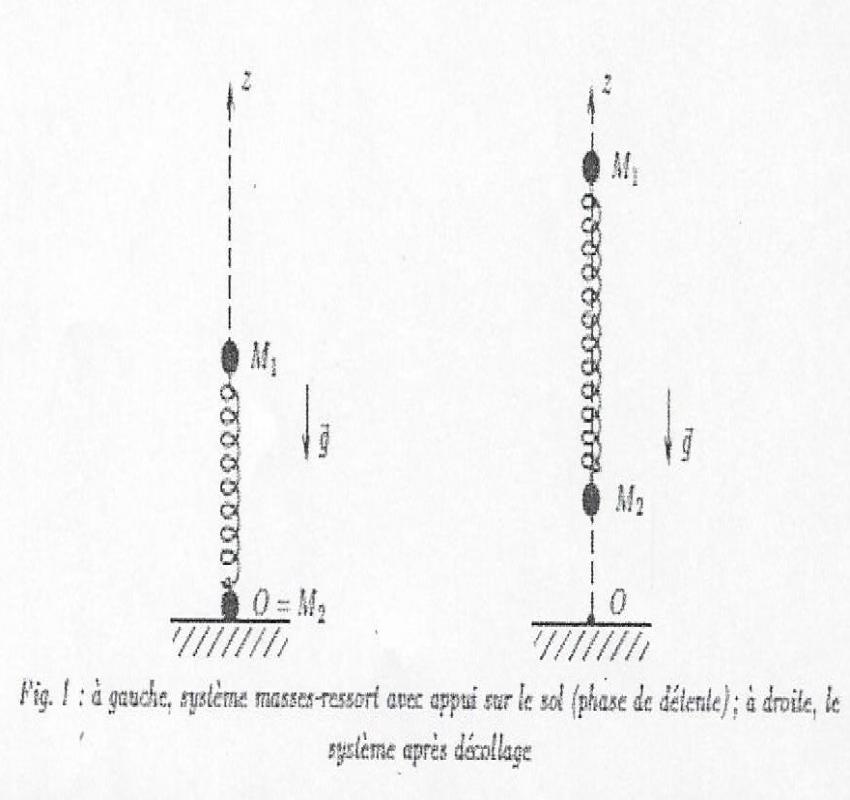
Le problème se pose sur un objet bondissant, modélisé par un ressort et deux masses, M1 et M2, reliées par un ressort de longueur l0 et de raideur k. Les altitudes des deux points sont respectivements z1(t) et z2(t).
1) faire le bilan des forces de M1 et M2 quand M2 est au sol, en fonction de k et l ,puis en fonction de k et z1(t)
Projection sur (O,z)
Pour M1  F = P+F
F = P+F
 ma = -mg - k (l-l0)
ma = -mg - k (l-l0)
 ma = -mg - k(z1(t)-l0)
ma = -mg - k(z1(t)-l0)
Pour M2  F = F car la force de réaction compense celle du poids
F = F car la force de réaction compense celle du poids
 ma = k ( l-l0)
ma = k ( l-l0)
2) Même chose pour M2 ayant décollé du sol
3) déterminer la longueur l1 lorsque M1 est à l'équilibre, M2 au sol
4) déterminer l'équation diférentielle z1(t) et explicité la pulsation propre w0 du mouvement de M1 et la résoudre pour pour la phase de détente.
ici je ne vois pas comment faire et je ne suis pas sûr d'avoir bien les bonnes équations de départ , surtout en fonction de z(t).
Merci d'avance à ceux qui voudront bien m'éclairer 
Bonsoir
Quelques indications qui pourront j'espère t'aider.
1° En considérant le ressort de masse négligeable, la relation fondamentale de la dynamique appliquée à celui-ci, combiné au principe des actions réciproques (action et réaction) permet de montrer que, dans tous les cas et à chaque instant, la force exercée sur le ressort sur M1 et la force exercée par le ressort sur M2 sont deux forces de vecteurs opposés, leur norme commune étant : k|l-lo| . Je te laisse algébriser cela...
Tant que M2 est immobile au sol, tu as effectivement :
La résolution de cette équation différentielle va faire intervenir la pulsation propre...
2° Toujours tant que M2 est au sol, tu as tord de dire que la réaction du sol compense le poids. Tu peux seulement dire que la résultante des trois forces appliquées (le poids, la réaction du sol, l'action du ressort) est le vecteur nul. Cela va te permettre d'exprimer l'intensité de la réaction du sol et c'est justement lorsque cette intensité va s'annuler que M2 va décoller... Mais tu n'en es pas encore là...
Donc ça donnerait pour le 1) :
M1a= -M1-k(z1-l0)
M2a=-M2g+k(z2-lo)+R
Et donc d'après ce principe on aurait : -M1-k(z1-l0) = -M2g+k(z2-lo)+R
Pour le 2) quand M2 n'est plus au sol :
M1a= -M1-k(z1-l0)
M2a=-M2g+k(z2-lo)+0 puisque la réaction n'est plus là
Si c'est bien ça, je ne vois pas comment avoir ni l1, ni ce que peut être la résolution du 4)
Je ne trouve pas le terme de pulsation propre dans mon cours, à quoi cela correspond ?
Bonjour
Un conseil : commence par traiter au brouillon tout ce qui concerne la situation où M2 est immobile sur le sol. L'ordre des questions de ton énoncé mélange les deux situations et ne respecte pas l'ordre chronologique.Cela risque de t'embrouiller...
Dans ce qui suit, je suppose M2 immobile au sol.
Concernant M1 dans la phase de détente du ressort : je ne suis pas sûr que tu ais compris que l'accélération a1 est la dérivée seconde de z1 par rapport au temps... L'équation différentielle que je t'ai écrite hier peut s'écrire, après division de tous les termes par M1 :
Soit, en posant :
La solution de cette équation est une somme de deux termes :
1° une solution particulière z1p correspondant au cas : c'est la solution correspondant à l'équilibre : z1p=l1 selon ton énoncé.
2° la solution correspondant au second terme nul, c'est à dire la solution de l'équation différentielle : . La solution est de la forme :
.
A et  sont deux constantes dépendant des conditions initiales ;
sont deux constantes dépendant des conditions initiales ;  o est la pulsation des oscillations dans ce cas où les frottements sont négligés ; c'est ce qu'on appelle la pulsation propre de l'oscillateur.
o est la pulsation des oscillations dans ce cas où les frottements sont négligés ; c'est ce qu'on appelle la pulsation propre de l'oscillateur.
La solution générale de l'équation différentielle est donc :
Je te laisse exprimer l1 en fonction des données...
Quand M2 est immobile au sol, son accélération est nulle et z2=0... On obtient donc :
Je suppose maintenant que M2 a décollé du sol.
La longueur du ressort est (z1-z2)
La relation fondamentale de la dynamique appliquée successivement aux deux masses conduit à :
Bon courage !
Merci ! ça m'éclaire un peu sur la chose. Dans le cours on nous propose cette formule :
x(t)=a/wo² + A*cos (wot+ )
)
mais on nous a dit de privilégier
x(t)=a/wo² +  cos(wot)+
cos(wot)+ sin(wot)
sin(wot)
En suivant la première j'obtiendrais :
l1= z1- A*cos(wot+ ) et du coup l1 c'est l0 je suppose non ?
) et du coup l1 c'est l0 je suppose non ?
mais je n'ai aucune donnée chiffrées pour calculer :/
En ce qui concercne la question 4) on a " la masse m1 est abaissée à l'altitude l1- l et l'ensemble est lâché sans vitesse initiale , on étudie la phase de détente ou M2 est au sol
l et l'ensemble est lâché sans vitesse initiale , on étudie la phase de détente ou M2 est au sol
) déterminer l'équation diférentielle z1(t) et explicité la pulsation propre w0 du mouvement de M1 et la résoudre pour pour la phase de détente.
Dans ce cas là la mesure du ressort est toujours z1(t) - z2(t) ?
je suis désolé si mes questions peuvent paraitre stupides
du coup l1 c'est l0 je suppose non
Tu n'as pas bien lu ce que j'ai écrit ! l1 est la longueur à l'équilibre que tu dois calculer à la question 3... Si dans l'équation différentielle, tu poses
En revanche, selon le choix des conditions initiales, il peut effectivement être intéressant de remplacer
A.cos(
 ot+
ot+ ) par
) par  .cos(
.cos( ot)+
ot)+ .sin(
.sin( ot).
ot).
Dans ce cas là la mesure du ressort est toujours z1(t) - z2(t) ?
Là non plus : tu n'as pas bien lu l'énoncé ! il s'agit d'établir l'expression de z1 lorsque M2 est au sol.
Il s'agit donc de trouver
 et
et  sachant que :
sachant que :
et :
et :
Donc d'après cela on a
 =-
=- l pour avoir l1=l1-
l pour avoir l1=l1- cos(0)
cos(0)
v(o)=0 donc
z1..=-wo
 sin(wo*0)+wo
sin(wo*0)+wo cos(wo*0)
cos(wo*0)
 0=
0= *1
*1

 =0
=0
Au final on aurait donc ceci ?
z1(t)= l1 +
 l*cos(wo*t)
l*cos(wo*t)Donc j'ai les équations de départ,
l1= lo-(g*M1)/k
z(t)=l1- l*cos(w0t)
l*cos(w0t)
où Wo est la pulsation à l'origine du ressort
5) Résoudre cette équation
c'est ce que je viens de faire je suppose ?
6) Montrer que si  l est inférieur à une valeur
l est inférieur à une valeur  lm, la composante Rz ne s'annule jamais
lm, la composante Rz ne s'annule jamais
Déterminer  lm en fonction de m1, m2, g et k
lm en fonction de m1, m2, g et k
On suppose qu'on est au dessus de  lm
lm
7) déterminer l'altitude z1d de M1 au décollage en fonction de l0, m1 et m2
montrer que quand m2=0 alors z1d tend vers l0
z1(t)=l1-
 l*cos(w0t)
l*cos(w0t)
où
 o est la pulsation à l'origine du ressort
o est la pulsation à l'origine du ressort  o est la pulsation propre de l'oscillateur constitué du ressort et de la masse M1. M2 n'intervient pas encore.
o est la pulsation propre de l'oscillateur constitué du ressort et de la masse M1. M2 n'intervient pas encore.
Ce que l'énoncé appelle Rz est ce que j'ai noté précédemment R. Je t'en ai fourni l'expression. Si R ne s'annule jamais, la masse M2 reste en permanence au sol.
Sinon, M2 décolle à l'instant où R s'annule...
On aurait alors cette relation 0=k(z_{1}-l_{0})-M_{2}.g+R
Mais je ne vois pas comment retrouver  Lo ainsi que la relation à trouver
Lo ainsi que la relation à trouver
Tant que M2 reste au sol, on peut écrire :
Dans l'expression de R, z1 apparaît précédé d'un signe "-". La valeur minimale que peut prendre R correspond dont à la valeur maximale que peut prendre z1 soit :
La valeur minimale théorique de R est ainsi :
Si Rmin est strictement positif, la valeur de R ne peut jamais s'annuler : M2 ne décolle jamais. Cela correspond à :
La valeur minimale théorique de R est ainsi :
R_{min}=M_{2}\cdot g-k\left(l_{1}+\Delta l-l_{0}\right)=\left(M_{1}+M_{2}\right)\cdot g-k\cdot\triangle l
Comment faites vous pour passer de la première égalité à la deuxième en introduisant M1 ?
Je pose la question car je ne suis pas sûr. Pour moi ça vient de la toute première équation avec le bilan des forces en M1
Pour la question 7 :
On veut z1d , ce qui correspond à R=0
 m2*g-k(z1-lo)=0
m2*g-k(z1-lo)=0
soit z1d=lo+(m2g)/k
On a donc bien, z1d=lo si m2 tend vers 0 ( mais j'ai toujours un k alors que ça doit être en fonction de l0,m2 et g  )
)
8)
on a m2=0 , au décollage du ressort on a l=lo fixe puisque m2 est à 0
Le système possède t-il encore de l'énergie élastique sans contact avec le sol ?
en utilisant un argument énergétique, déterminer z1max du bond que réalise M1 en fonction de :m1,g,k,lo et  l
l
Pour moi je pense qu'elle en a toujours, mais je ne vois pas comment passer par l'énergétique pour avoir z1max
Il faut écrire la conservation de l'énergie mécanique entre l'instant initial et l'instant où z1 est maximum.
Instant initial :
Instant d'altitude z1max : le ressort n'exerce plus de force ; il a la longueur lo :
En écrivant que l'énergie mécanique est la même dans les deux cas, on obtient l'expression de z1max
On a donc plus d'énergie potentielle élastique quand on quitte le sol ?
Ca donnerait Z1max = lo- l-m1g/k+ (1/2)k(
l-m1g/k+ (1/2)k( l+m1g/k)²/mg
l+m1g/k)²/mg
Validé ?
On a donc plus d'énergie potentielle élastique quand on quitte le sol ?
Lorsque le ressort n'est plus en contact avec le sol, il reprend sa longueur à vide l0. L'énergie potentielle élastique devient nulle.
Revois ton calcul de l'altitude max ; attention aux parenthèses ; il y a une simplification. La masse est M1, pas m. Selon moi :


