Inscription / Connexion Nouveau Sujet
Oscillateur harmonique
Bonjour !
J'ai un petit exercice et quelques résultats me paraissent... étranges... Pourriez vous m'aider ?
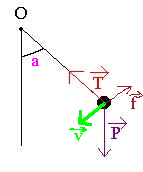
C'est un point matéreil M de masse m accroché à un point fixe par l'intermédiaire d'un fil inextensible qui fait un angle a avec l'horizontale. Conditions initiales : angle a0 et vitesse initiale nulle. On note f=-n*v les frottements.
On doit établir l'équa diff, c'est fait : (d2a/dt2)+(2/tau)(da/dt)+w02a=0
Je trouve l'expression de tau : tau=2m/n, c'est la constante de temps du système mais quel est le sens de "donner son interprétation physique" ?
Je vous passe les autres questions étant donné que je les ai réussies et qu'elles n'ont pas d'importance pour mon problème.
Voici le tableau
| points | A | B | C | D |
| temps (s) | 0.53 | 1.1 | 2.2 | 8.25 |
| angle | 0 | 8.95 | 8.02 | 0 |
Et le graphique. Je vais tenter de vous le décrire étant donné que le scan n'est pas toléré... Ce sont les oscillations amorties qui sont réprésentées. Ca commence à 10° et décroît. A se situe à la première intersection de l'axe des temps avec la courbe REMONTANTE. B et C sont les deux premiers maximums atteints par la courbe après le début de l'enregistrement et enfin D se situe à 7 périodes exactement de A.
Je dois avec tout ça calculer le décrément logarithmique. Alors j'ai pris ln(a(t=1.1)/a(1.1+1.1)) (j'ai pris T=1.1 parce que B est le premier "sommet" après le départ...)
Calculer la pseudo période c'est bon
Calculer le temps tau ? J'ai pris T sur le décrément logarithmique mais comme ces deux là c'est moi qui les ai calculé, je dois pas faire autrement ??
Calculer la constante n des frottements, idem j'ai pris tau=2m/n mais ai-je le droit ?
Merci d'avance pour vos idées =)
étant donné que le scan n'est pas toléré...
Le scan de l'énoncé entier n'est pas admis, en revanche le scan du graphique joint, oui !
C'est un point matériel M de masse m accroché à un point fixe par l'intermédiaire d'un fil inextensible qui fait un angle a avec l'horizontale.
Conditions initiales : angle a0 et vitesse initiale nulle.
J'ai du mal à saisir... En fait, c'est donc un pendule simple sauf qu'on repère l'angle par rapport à l'horizontal et non par rapport à la verticale habituellement...
Si vous pouviez donner ces informations, cela serait utile pour vous aider ! Merci !
Mince j'ai mis horizontale Oho Non c'est bien par rapport à la verticale. C'est un angle a qui est fixe.
C'est un angle a qui est fixe.
Je pense plutôt qu'il est variable et que c'est a0 qui est fixé !
Donc c'est la situation que je vous ai jointe.
Pour le décrément logarithmique, par définition, c'est
= ln 
.T
Donc on mesure l'écart d'amplitude à une période d'intervalle. On en prend le log népérien et ça donne
Pour T, mesurer la sur votre graphique, tout simplement !
Une équation différentielle amortie est du type :
d²a/dt + 2.
.da/dt + 
0².a = 0
Donc pour votre exercice,
= 1/
pour une équation différentielle, si je ne me trompe pas,
d²a/dt² + (n/m).da/dt + (g/l).a = 0
Par identification, on a donc
= 1/ = 2m/n
ce qui rejoint bien ce que vous avez écrit :
Calculer la constante n des frottements, idem j'ai pris tau=2m/n mais ai-je le droit ?
Merci =)
Mais en fait ma question c'était "est-ce que je peux faire autrement pour trouver tau ou est-ce que je suis obligée de prendre ce que j'ai calculé juste avant" Et a ce que je vois c'est ce que je dois faire =)
A oui et pour le décrément logarithmique ce qui m'embete c'est qu'on me le demande avant la pseudo période et pourtant j'en ai besoin pour le calculer !
Dernière question : que dois-je répondre à "Donner l'interprétation physique de tau" ??
Merci et bonne année au fait =)
pour le décrément logarithmique ce qui m'embete c'est qu'on me le demande avant la pseudo période et pourtant j'en ai besoin pour le calculer !
Non, tu n'as pas besoin d'avoir T avant de calculer
.
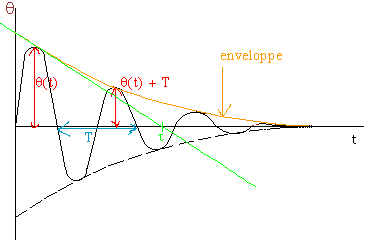
se détermine par méthode graphique et en utilisant sa définition (qui provient de l'équation de l'enveloppe des oscillations)
Donc ce que tu fais (voir courbe plus bas) :
1) Tu détermines graphiquement l'amplitude maximale à un instant donné.
2) Tu détermines graphiquement l'amplitude maximale une période plus tard
3) Tu appliques la fomule
= ln( 
(t) / [(t) + T]
4) Tu détermines graphiquement la valeur de la pseudo-période T
5) Ton amortissement est donné par la formule :
= T/ d'où le calcul de .
(et tu pourra peut-être vérifier qu'il est bien égal à 2m/n si tu connais la valeur de n, ce qui n'est généralement pas le cas).
"est-ce que je peux faire autrement pour trouver tau ou est-ce que je suis obligée de prendre ce que j'ai calculé juste avant"
A part le calculer en connaissant m et n, je ne vois pas... Mais comme souvent, on n'a pas la valeur du coefficient de frottement (et c'est normal, ça dépend des types de frottements).
Personnellement, je ne vois pas d'autre méthode.
"Donner l'interprétation physique de tau" ??
Comme le décrément
est un nombre sans dimension qui est égal à T/ d'après ton exercice.
On en déduit que
est homogène à un temps qu'on va appeler temps de relaxation caractéristique (ou constante de temps) de l'amortissement.
Comment on le visualise ?
Si tu traces l'enveloppe supérieure de la décroissance de tes oscillations, tu as une courbe mathématique dont l'epression est A.exp(-t/
) (d'où la formule du calcul du décrément)
C'est comme pour les décharges RC ou les décroissances radioactives, ...
On trace la tangente à cette enveloppe en t = 0. Elle coupe l'axe des temps en t =
Si je ne me trompe pas, elle te donne le temps au bout duquel ton amplitude d'oscillation a diminué de 63%.
(sauf erreur de ma part et bonne année !)
D'accord, en fait pour le décrément, grossièrement dit, c'est "une des périodes". C'est pas forcément celle que je calcule après...
Pour l'interprétation physique c'est OK aussi.
Merci beaucoup pour tout ce que vous avez fait !!!
Effectivement, pas forcément celle que tu calcules... Tu fais ça entre deux périodes successives car de toute façon, le ln( ) linéarise ton expression donc du coup, ça revient au même !
Tu pourrais même le faire sur un nombre n de période car dans ce cas (pour plus de précision en général), tu aurais n fois ton décrément...
Pour preuve, d'après l'équation de l'enveloppe :
A l'instant (t) A.exp(-t/)
A l'instant (t + nT) A.exp(- [t+N.T]/) = A.exp(-t/).exp(-nT/)
Donc le rapport devient :
r = A.exp(-t/) / A.exp(-t/).exp(-nT/) = 1/exp(-nT/) = exp(nT/)
Et en linéarisant par la fonction ln pour obtenir un décrément 
sur n périodes :
= ln(r) = nT/ = n 
avec le décrément que tu cherches 
Annuler
connectez vous