Inscription / Connexion Nouveau Sujet
Oscillateur
Bonjour,
J'aurais besoin de votre aide concernant l'exercice suivante.
Merci d'avance pour votre aide.
Soient deux points matériels et
de masses respectives
et
, reliés par un ressort de constante de raideur
et de longueur à vide
. Ils peuvent glisser sans frottement sur un axe horizontal
fixe dans le référentiel terrestre supposé galiléen.
Un allongement initial du ressort ayant été produit, on abandonne le système immobile dans le référentiel terrestre supposé galiléen.
Soit . Donner l'expression de l'énergie mécanique du système
.
___________________________________________________________________________________________________________
Je trouve comme expression de l'énergie mécanique :
(somme des énergies potentielle et cinétique).
Sauf que je n'arrive pas à faire apparaître là-dedans. Tout du moins pas dans l'expression de l'énergie cinétique.
J'aboutis à car
.
Merci d'avance.
Comment calcules-tu les "énergies potentielles"? à quoi correspondent-elles?
De même pour l'expression de l'énergie cinétique? D'où vient-elle?
L'énergie potentielle d'un ressort est où
est l'allongement du ressort.
Après l'énergie cinétique est avec
la masse de l'objet et
sa vitesse. Or ici la vitesse a une seule composante qui est selon
. D'ailleurs j'ai oublié de mettre les points au-dessus des
parce qu'il s'agit de la dérivée de la position par rapport au temps... Désolé pour la faute de frappe.
Je suis d'accord pour l'expression de l'énergie cinétique si tu utilises bien les vitesses.
Ton expression de l'énergie potentielle est correcte aussi dans ton second message (même s'il manque la constante de raideur  ). Par contre, dans ton premier message, pourquoi as-tu deux expressions qui apparaissent dans l'énergie mécanique avec des signes différents?
). Par contre, dans ton premier message, pourquoi as-tu deux expressions qui apparaissent dans l'énergie mécanique avec des signes différents?
Il te suffit d'utiliser et d'exprimer
en fonction de
et
...
Après relecture et correction, j'obtiens .
Auparavant j'avais également établis l'équation différentielle vérifiée par avec
.
Sa solution est .
Dans la suite du problème, on considère cette fois l'énergie potentielle d'intéraction du système définie par
avec
et
un coefficient positif ou négatif.
Déterminer l'équation différentielle vérifiée par (on fera apparaître la pulsation
introduite précédemment).
Sauf que je ne vois vraiment pas comment m'y prendre. Avez-vous une idée ?
Merci d'avance  .
.
On te demande vraisemblablement de faire exactement la même chose que tu as fait pour établir l'équation différentielle précédente, mais cette fois pour une énergie potentielle s'exprimant sous une forme différente.
Bonjour donaldos,
Pour obtenir la première équation différentielle, j'avais utilisé le P.F.D. que j'avais ensuite projeté.
Il ne s'agit donc pas de la même méthode ici...
Une idée ? Merci d'avance.
Ne vois-tu pas une ressemblance entre les deux expressions de ?
Si je te dis que chacune des masses est soumise à une force c'est plus facile?
Merci beaucoup donaldos  , je n'avais pas pensé à procéder de cette manière.
, je n'avais pas pensé à procéder de cette manière.
Je trouve donc comme équation différentielle vérifiée par :
avec toujours
.
Maintenant, je dois représenter graphiquement l'allure de en précisant les extrema puis montrer que la solution
ne peut être périodique que si l'énergie mécanique totale
du système est inférieure à une valeur que l'on précisera.
Moi je ne vois qu'un extremum pour . Mais je ne vois pas comment trouver la valeur limite pour que la solution soit périodique... Merci d'avance pour votre aide.
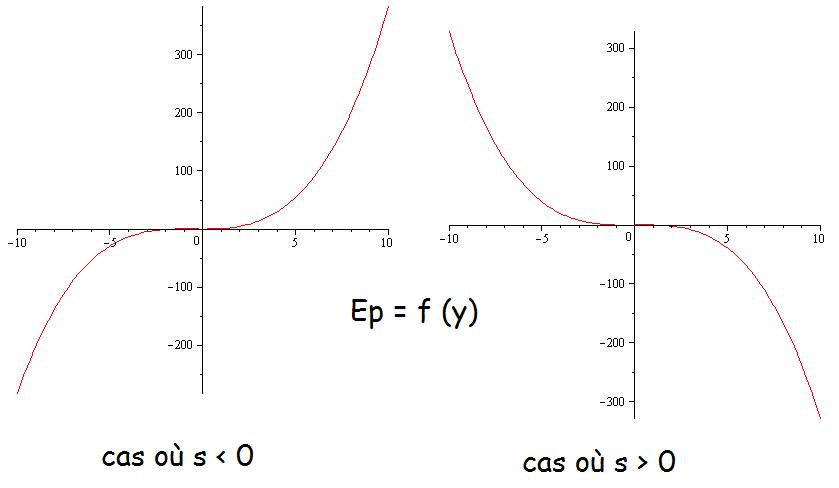
Es-tu sûr de tes représentations? L'énergie potentielle doit s'annuler en une autre valeur de (qui dépend de
).
C'est bon, je trouve un maximum et un minimum d'énergie potentielle. La position correspond à un équilibre stable.
ne peut donc être périodique que si
qui est la valeur du maximum d'énergie potentielle.
Par contre je ne comprends pas trop la suite...
___________________________________________________________________________________________________________________________
On se place dans la cas où l'on a de petites oscillations autour de la position d'équilibre stable.
En choisissant convenablement l'origine des temps, on montre qu'on peut rechercher une solution de l'équation différentielle vérifiée par , obtenue précédemment, de la forme
où
et
sont des constantes non nulles à déterminer en précisant les approximations à faire pour obtenir la forme souhaitée.
Montrer qu'alors .
___________________________________________________________________________________________________________________________
D'après la question précédente, j'ai donc comme position d'équilibre. Mais je ne vois pas quelles approximations faire... D'habitude on a des cosinus, sinus ou tangente que l'on peut approximer dans les conditions de Gauss mais là...
Auriez-vous une idée ? Pour rappel, l'équation différentielle vérifiée par est
avec
.
Merci d'avance  .
.


