Bonsoir
Attention à ne pas confondre orbitale atomique (région de l'espace entourant le noyau telle que la probabilité cumulée d'y trouver l'électron est de 95% ) et la fonction d'onde .
J'imagine que l'expression que tu fournis est la fonction d'onde de l'orbitale atomique 3s. Es-tu bien sûr de ton expression ? Les sites que je viens de consulter (celui-ci par exemple : ) fournissent une expression différente.
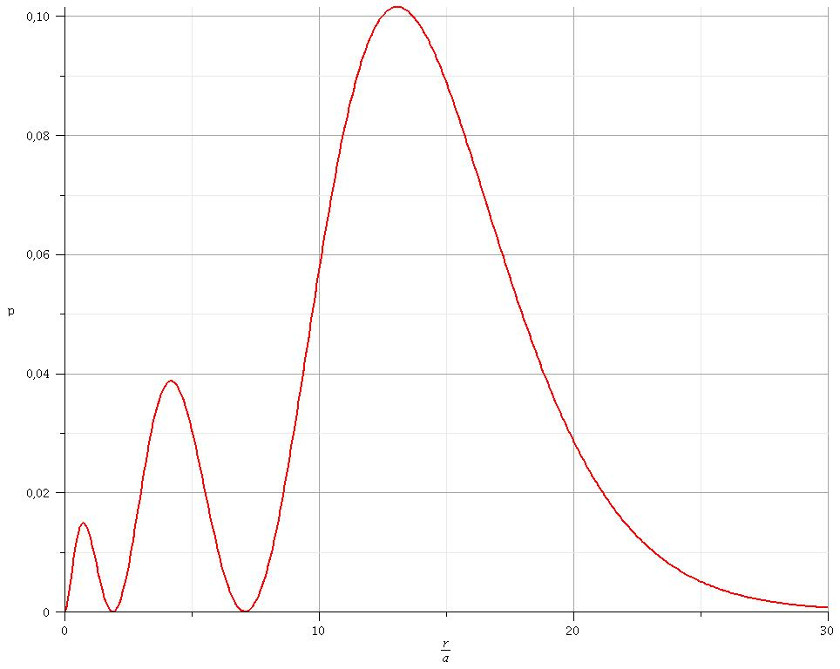
Tu parles ensuite d'extrema. La méthode d'obtention est celle habituellement utilisée en math : calcul de la dérivée par rapport à r et tableau de variations. Reste à savoir quelle fonction étudier... en fonction de r peut s'étudier mais présente assez peu d'intérêt. Il est plus intéressant d'étudier les variations en fonction de r de la densité de probabilité : p(r)=4.r².² ; en effet : p(r).dr représente la probabilité que l'électron soit présent entre les sphères centrée sur le noyau de rayon r et de rayon (r+dr). La probabilité que l'électron soit présent en un point quelconque de l'espace étant égale à 1, la fonction d'onde doit être normée :


C'est bien le cas de la fonction d'onde _3s figurant sur le site que je viens de t'indiquer, ce n'est pas le cas de celle que tu indiques.
Pour info : voici la représentation de p en fonction de

Bonjour,

Effectivement je me suis trompé sur l'exponentielle. C'était e^(-r/3a0)

Merci beaucoup !