Inscription / Connexion Nouveau Sujet
optique géométrique
Bonsoir, je rencontre des difficultés pour débuter cet exercice. merci d'avance pour l'aide.
un bassin est rempli d'eau sur une hauteur AB de 5m. sur quelle longueur minimale BC doit-on couvrir la surface de l'eau pour que le mur AB soit invisible pour un observateur situé au dessus du bassin ?
je pense qu'il faut utiliser le loi de Snell Descartes mais nous avons aucune mesure d'angle
bonsoir vanoise
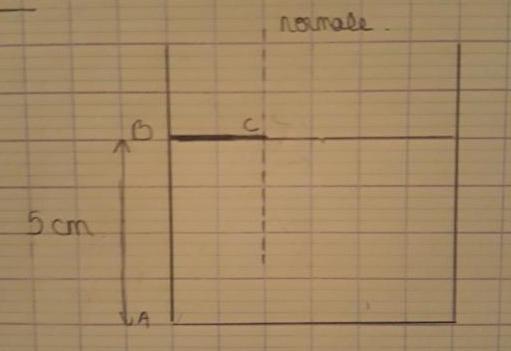
voici mon schéma
loi de snell descarte
n1 * sin i1= n2 * sin i2
n1= 1,5
n2 = 1,33
mais je ne sais vraiment pas quoi mettre pour i1 et i2
Revois ton cours sur les notions de réfraction limite et de réflexion totale. Pour que le mur soit invisible d'un observateur situé au dessus de l'eau, il faut que tous les rayons partant du mur et arrivant à la surface de l'eau à droite du point C subissent une réflexion totale et non une réfraction.
le rayon réfracté n'existe plus pour une valeur limite fixée par
sin i lim = n2/n1 = 1.33/1.5
i lim = arcsin (1.33/1.5)
i lim = 62.4 °
il faut que l'observateur se positionne à 62.4 ° pour que le mur AB soit invisible.
est-ce cela ?
Tu peux exprimer le sinus de l'angle d'incidence pour le rayon AC en fonction des distances AB et BC.
Pour que B ne soit pas visible d'un observateur situé au dessus, ce rayon ne doit pas sortir de l'eau ; il doit donc subir une réflexion totale.
sin i = BC/ AC ?
je ne comprends pas pourquoi le point B ne doit pas etre visible. je pensais que s'était le point A
Oui pour le sinus. La longueur AC s'obtient en fonction de BC et h=5m (pas 5cm selon l'énoncé) par application du théorème de Pythagore.
Tous les rayons arrivant en C et partant des points du murs situés entre B et C arrive en C avec un angle d'incidence supérieur à celui que tu viens de calculer. Si le rayon AC subit une réflexion totale, il en sera de même de tous les rayons partant d'un point quelconque du mur et arrivant en C. Si le point B n'est pas visible d'un observateur situé au-dessus de l'eau, il en sera de même de tous les points du mur situés entre A et B.
Remarque : une fois étudiée la situation du rayon AC, tu pourras aussi te demander ce qui se passe pour les rayons issus du mur et arrivant à la surface de l'eau en des points situés à droite du point C.
Comme déjà dit : pour bien comprendre cet exercice, il faut avoir bien compris les notions de réfraction limite et de réflexion totale.
bonjour
sin i = BC/AC BC=sin i *AC
AC²=5² + BC² = 5²+ (sin i *AC)²= 5² + (sin i )²*AC²
je peux diviser par AC² de chaque côté ?
je peux diviser par AC² de chaque côté ?
Non : comme déjà dit, il faut utiliser le théorème de Pythagore :
AC2=h2 + BC2
N'oublie pas que le calcul se fait dans le cas de la réfraction limite :
Je ne vois pas ce que l'indice du verre vient faire ici avec un énoncé tel que tu l'as copié.
Si tu as des problèmes avec le théorème de Pythagore et son application, une fois calculé le sinus de l'angle limite, tu peux en déduire la tangente puis utiliser la relation simple :


